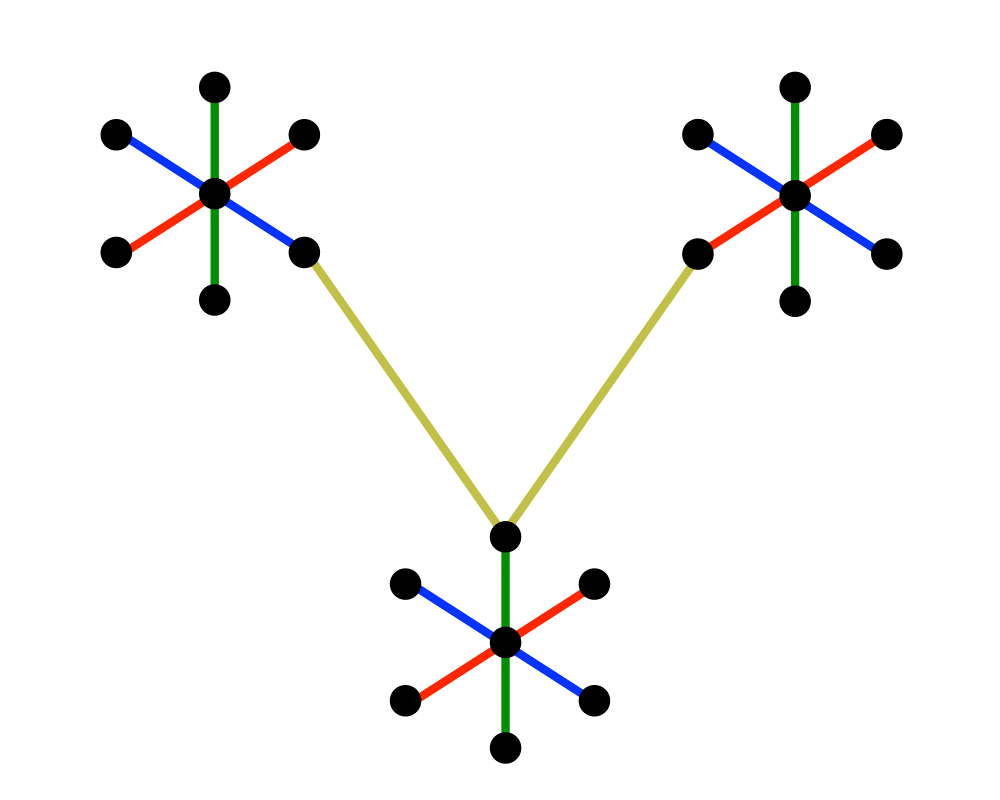Input

Output

Input Description: A graph \(G = (V,E)\) with weighted edges.
Problem: The subset of \(E\) of \(G\) of minimum weight which forms a tree on \(V\).

Excerpt from The Algorithm Design Manual: The minimum spanning tree (MST) of a graph defines the cheapest subset of edges that keeps the graph in one connected component. Telephone companies are particularly interested in minimum spanning trees, because the minimum spanning tree of a set of sites defines the wiring scheme that connects the sites using as little wire as possible. It is the mother of all network design problems.

Minimum spanning trees prove important for several reasons:

• They can be computed quickly and easily, and they create a sparse subgraph that reflects a lot about the original graph.
• They provide a way to identify clusters in sets of points. Deleting the long edges from a minimum spanning tree leaves connected components that define natural clusters in the data set, as shown in the output figure above.
• They can be used to give approximate solutions to hard problems such as Steiner tree and traveling salesman.
• As an educational tool, minimum spanning tree algorithms provide graphic evidence that greedy algorithms can give provably optimal solutions.

Implementations

Boost Graph Library (rating 10)	C++ Boost Library (rating 10)
algorithms.js (rating 9)	java-algorithms-implementation (rating 9)
JDSL (rating 8)	goraph (rating 7)
Moret and Shapiro's Algorithms P to NP (rating 7)	Stanford Graphbase (rating 7)
LEDA (rating 5)	Netlib (rating 5)

Recommended Books

Geometric Spanner Networks by G. Narasimhan and M. Smid	Spanning Trees and Optimization Problems by B. Wu and K Chao	Algorithms in Java, Third Edition (Parts 1-4) by Robert Sedgewick and Michael Schidlowsky
Computational Geometry : Algorithms and Applications by Mark De Berg, Marc Van Kreveld, Mark Overmars, and O. Schwartskopf	Network Flows : Theory, Algorithms, and Applications by Ravindra K. Ahuja, Thomas L. Magnanti, and James B. Orlin	Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica by S. Pemmaraju and S. Skiena
Computational Geometry by F. Preparata and M. Shamos	Combinatorial Optimization: Algorithms and Complexity by C. Papadimitriou and K. Steiglitz	Combinatorial Optimization: Networks and Matroids by E. Lawler

Related Problems

Set Data Structures

Steiner Tree

Traveling Salesman Problem

As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.