 |
 |
|
|
Input Description: A function \(f(x_1,...,x_n)\).
Problem: What point \(p = (p_z,...,p_n)\) maximizes (or equivallently minimizes) the function \(f\)?
Excerpt from The Algorithm Design Manual: Optimization arises whenever there is an objective function that must be tuned for optimal performance. Suppose we are building a program to identify good stocks to invest in. We have available certain financial data to analyze, such as the price-earnings ratio, the interest and inflation rates, and the stock price, all as a function of time \(t\). The key question is how much weight we should give to each of these factors, where these weights correspond to coefficents of a formula:
Unconstrained optimization problems also arise in scientific computation. Physical systems from protein structures to particles naturally seek to minimize their ``energy functions.'' Thus programs that attempt to simulate nature often define energy potential functions for the possible configurations of objects and then take as the ultimate configuration the one that minimizes this potential.
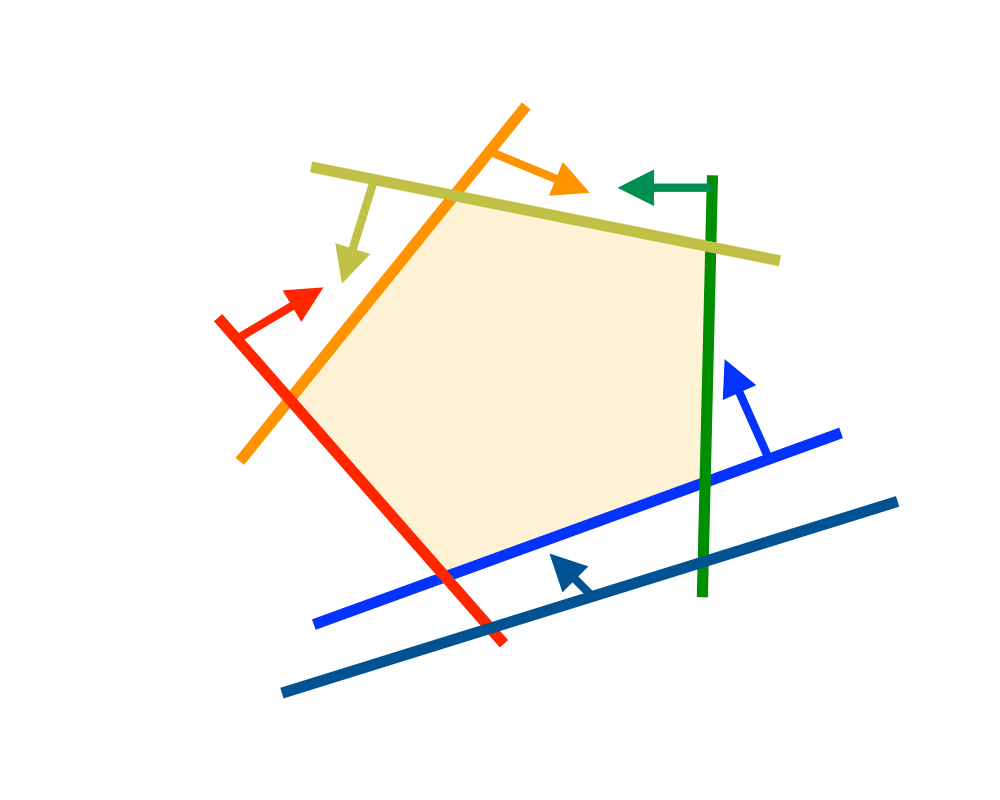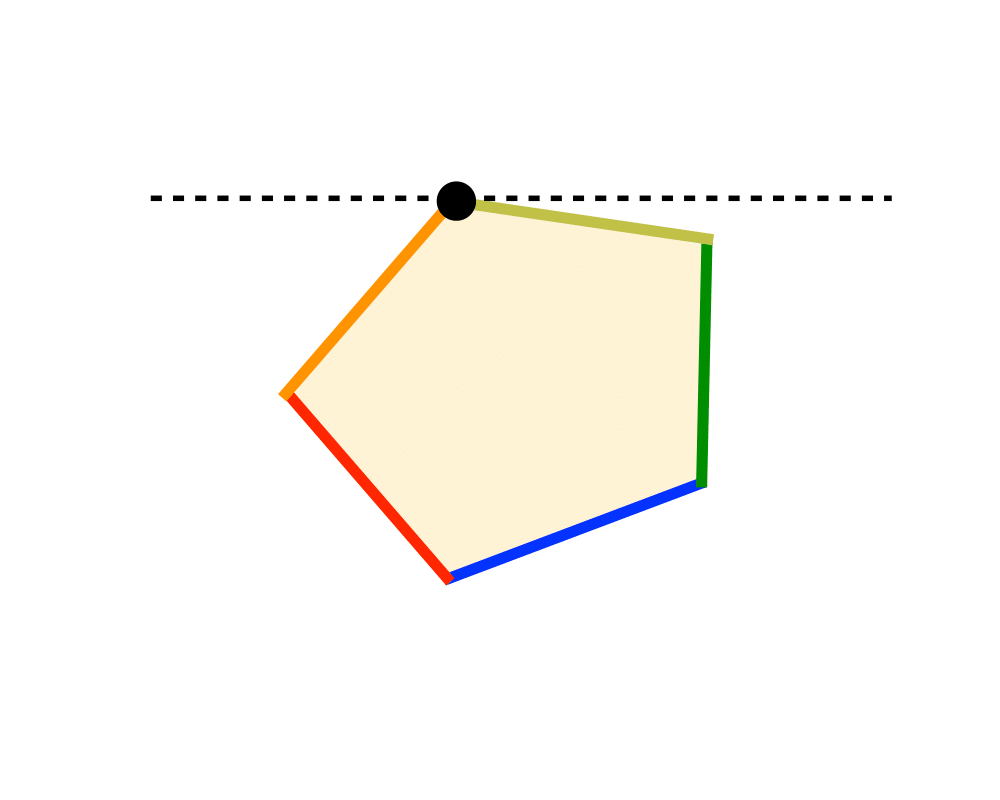  Linear Programming |
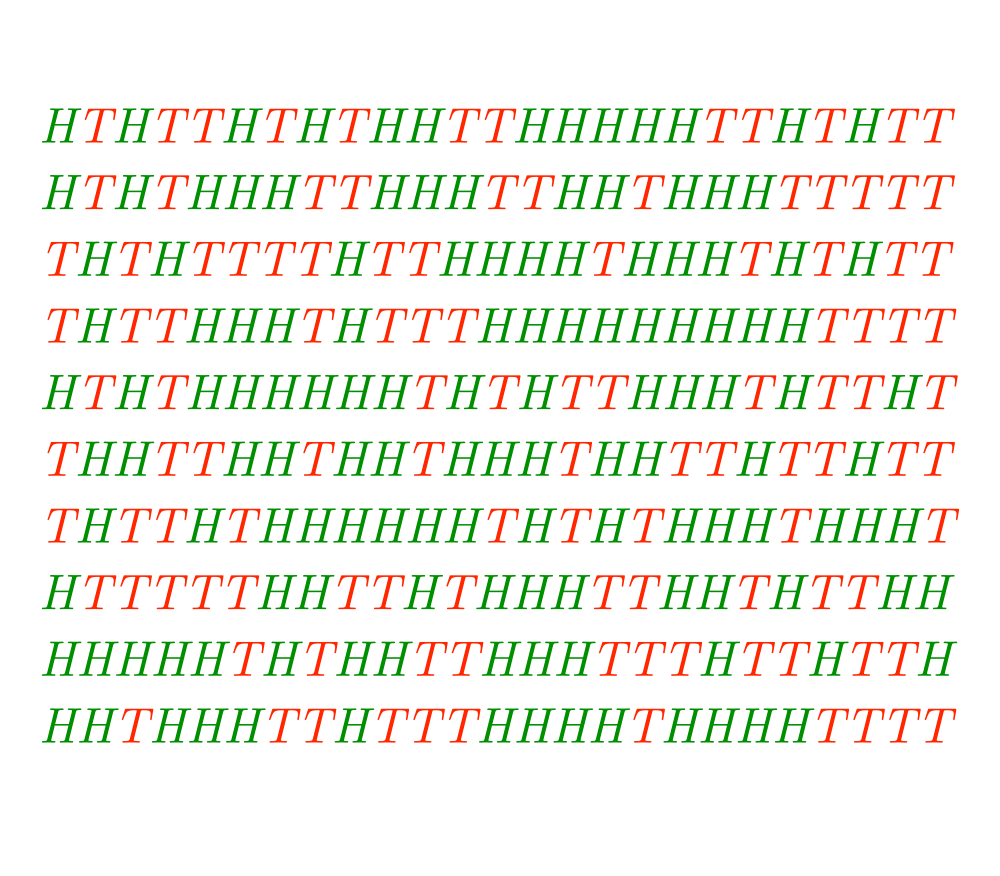  Random Number Generation |
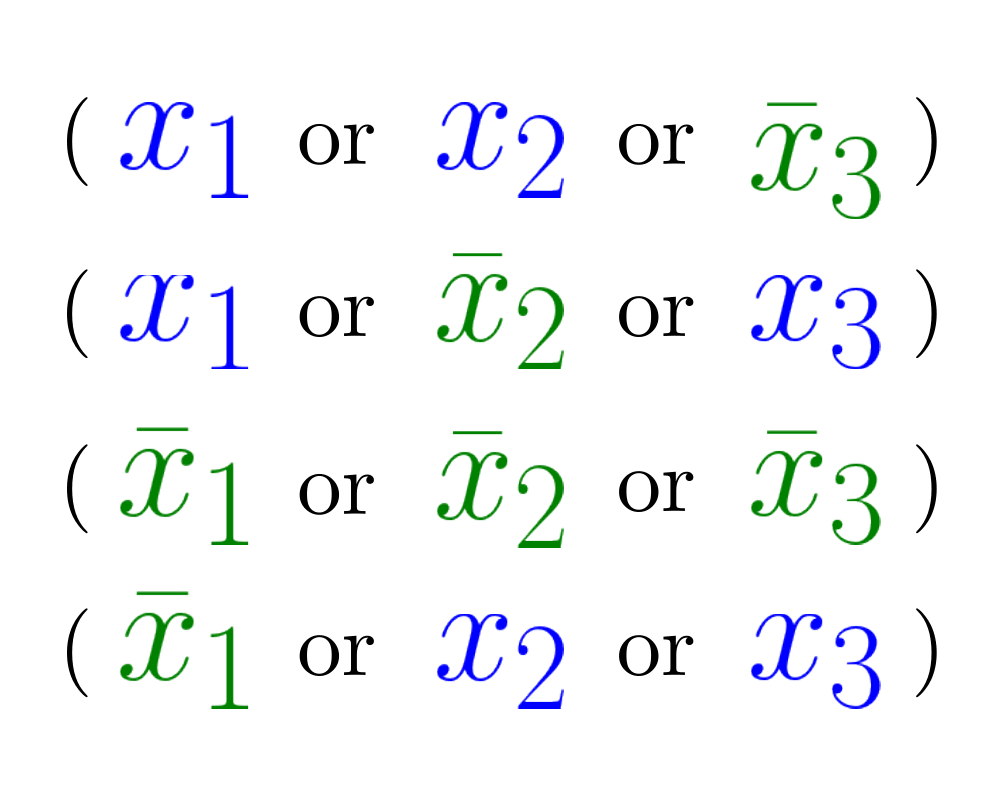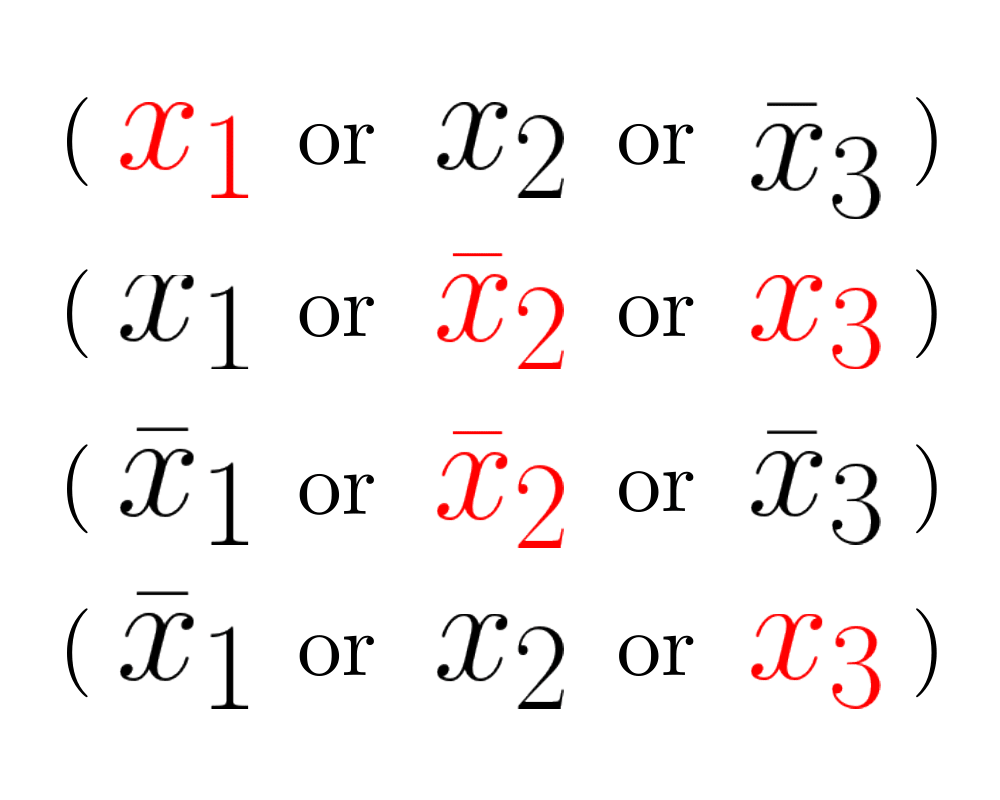  Satisfiability |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
Foundations of Genetic Programming by W. Langdon and R. Poli
How to Solve it: Modern Heuristics by Z. Michalewicz and D. Fogel
Local Search in Combinatorial Optimization by E. Aarts and J. K. Lenstra
Numerical methods and analysis by J. Buchanan and P. Turner
Practical Methods of Optimization: Unconstrained Optimization by R. Fletcher
Adaptation in Natural and Artificial Systems by J. H. Holland
Algorithms for minimization without derivatives by R. Brent