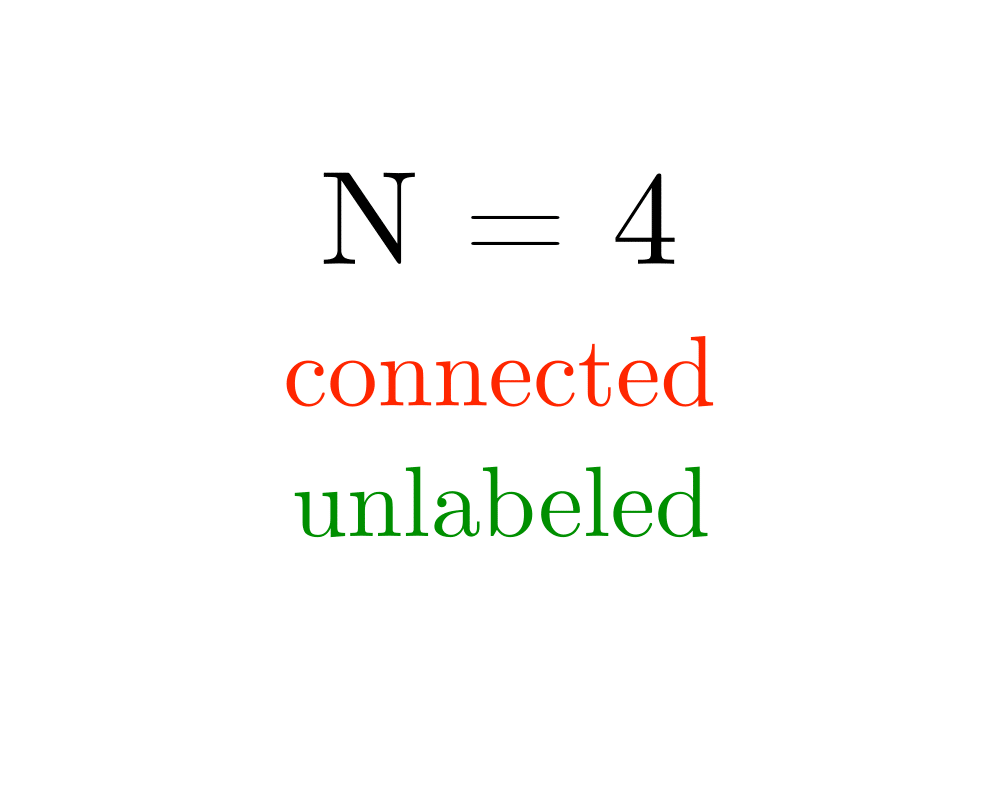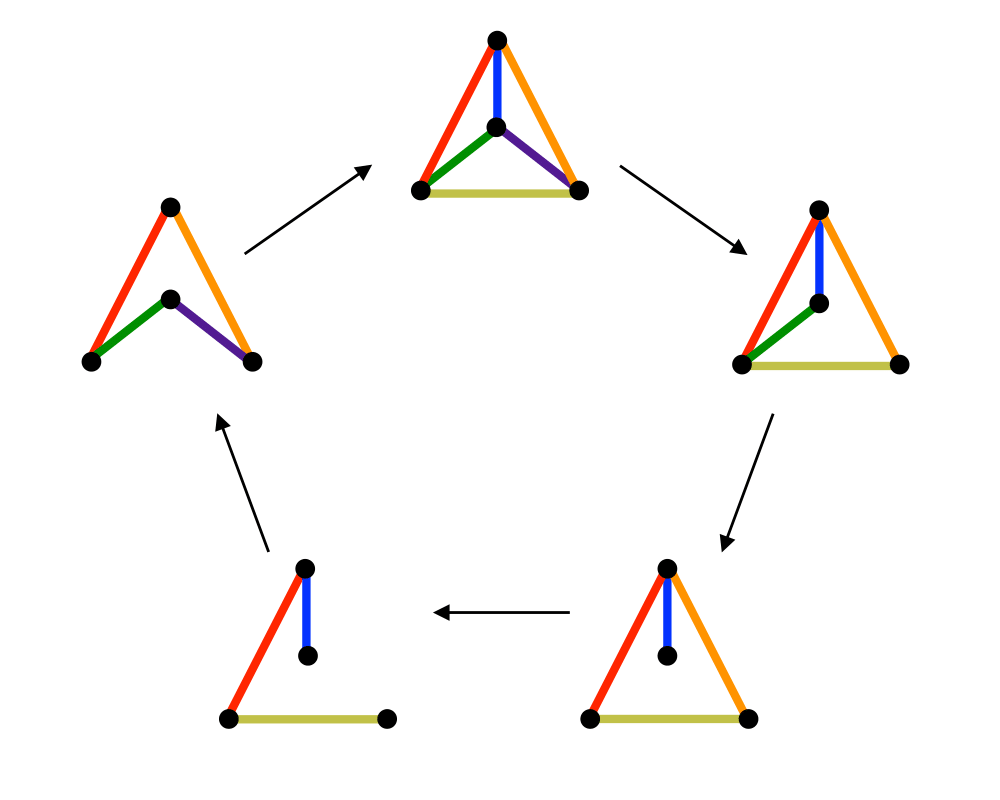
 |
 |
|
|
Input Description: Parameters describing the desired graph, such as the number of vertices \(n\), the number of edges \(m\), or the edge probability \(p\).
Problem: Generate (1) all, or (2) a random, or (3) the next graph satisfying the parameters.
Excerpt from The Algorithm Design Manual: Graph generation typically arises in constructing test data for programs. Perhaps you have two different programs that solve the same problem, and you want to see which one is faster or make sure that they always give the same answer. Another application is experimental graph theory, verifying whether a particular property is true for all graphs or how often it is true. It is much easier to conjecture the four-color theorem once you have demonstrated 4-colorings for all planar graphs on 15 vertices.
A different application of graph generation arises in network design. Suppose you need to design a network linking ten machines using as few cables as possible, such that the network can survive up to two vertex failures. One approach is to test all the networks with a given number of edges until you find one that will work. For larger graphs, more heuristic approaches, like simulated annealing, will likely be necessary.
| Stanford GraphBase (rating 10) |
Stanford Graphbase (rating 10) |
| CAGES (rating 9) |
Frank Ruskey's Combinatorial Generation Resources (rating 8) |
| Viger (rating 7) |
NAUTY (rating 7) |
| Combinatorica (rating 7) |
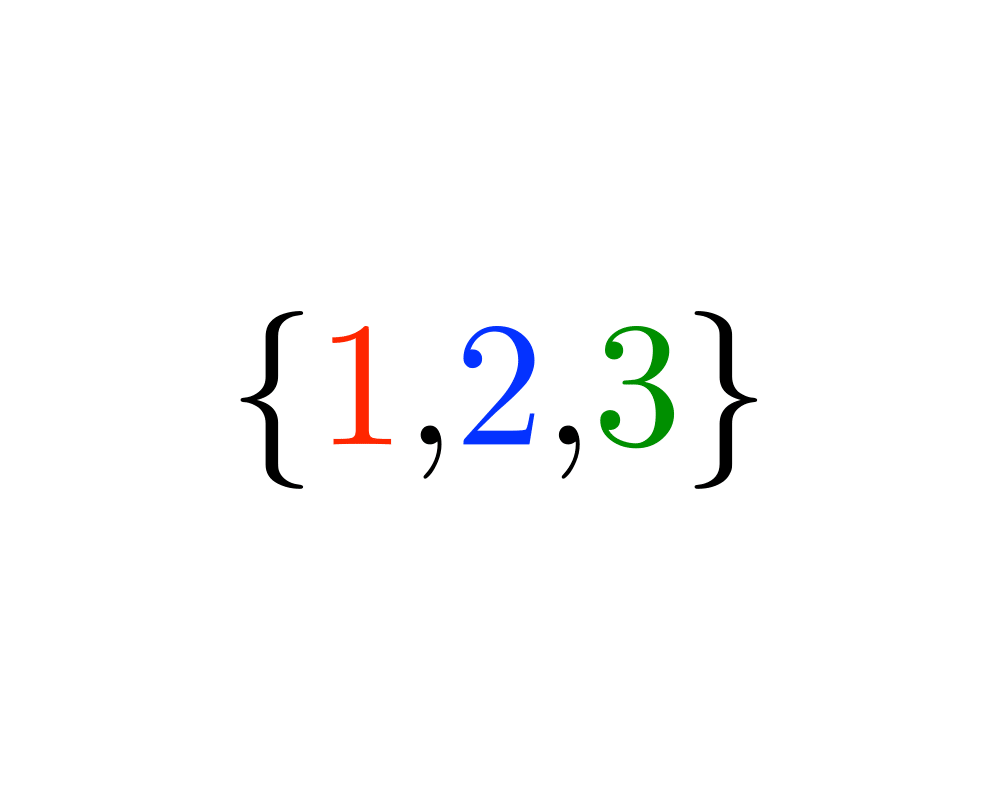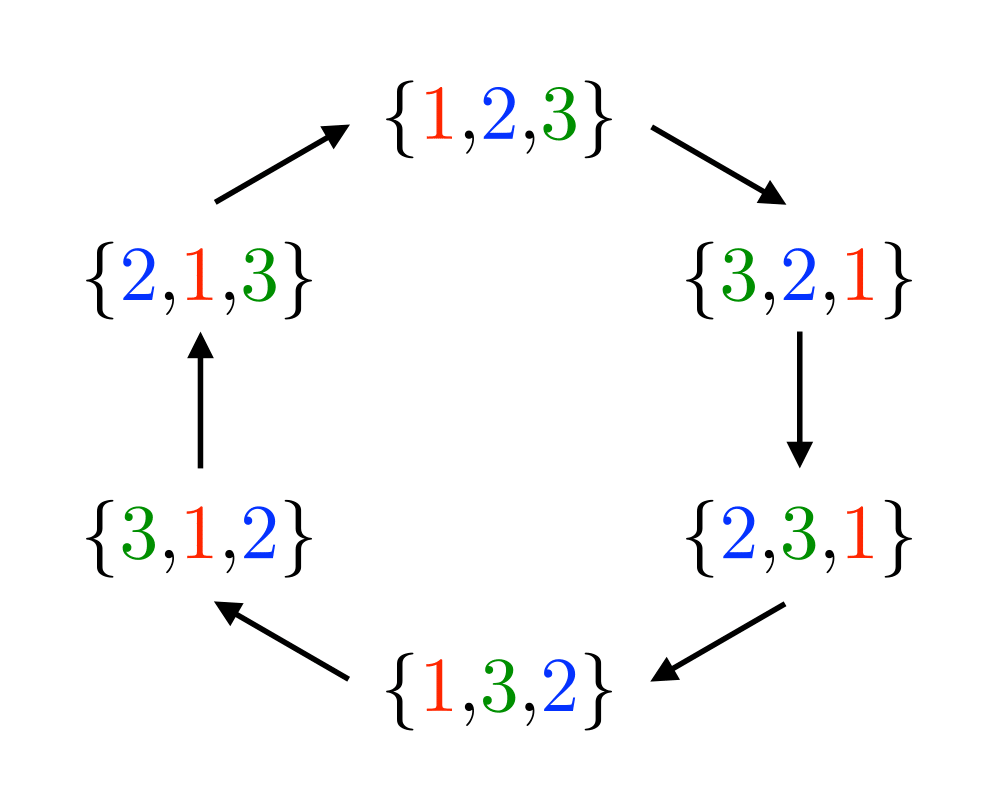  Generating Permutations |
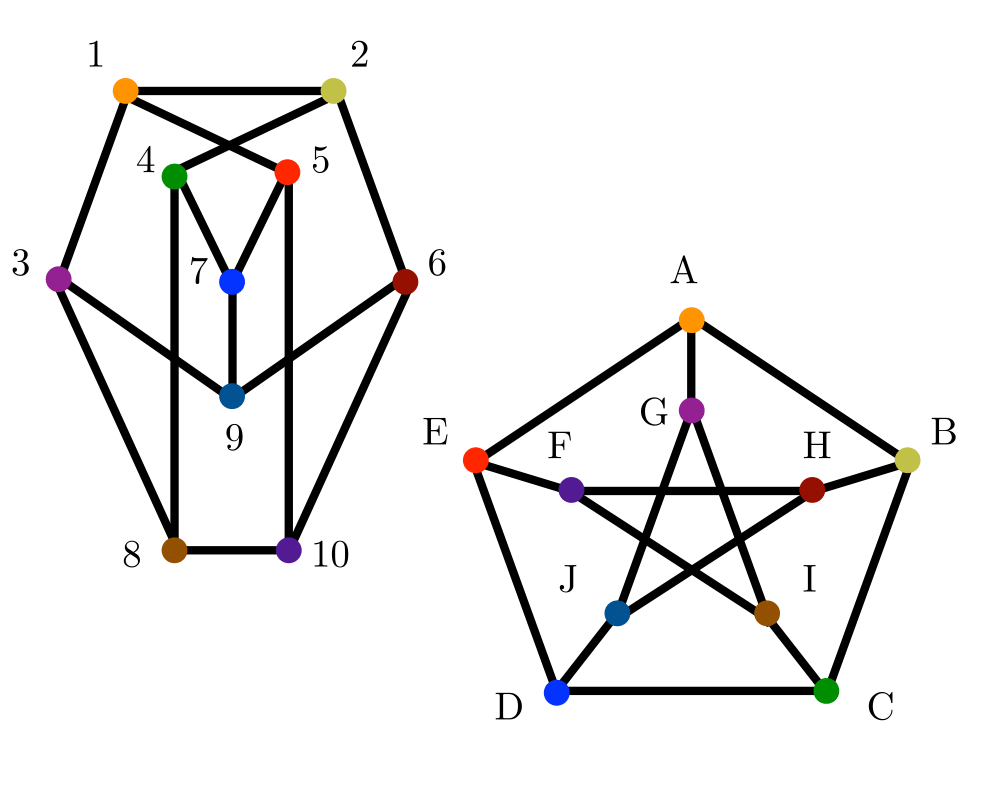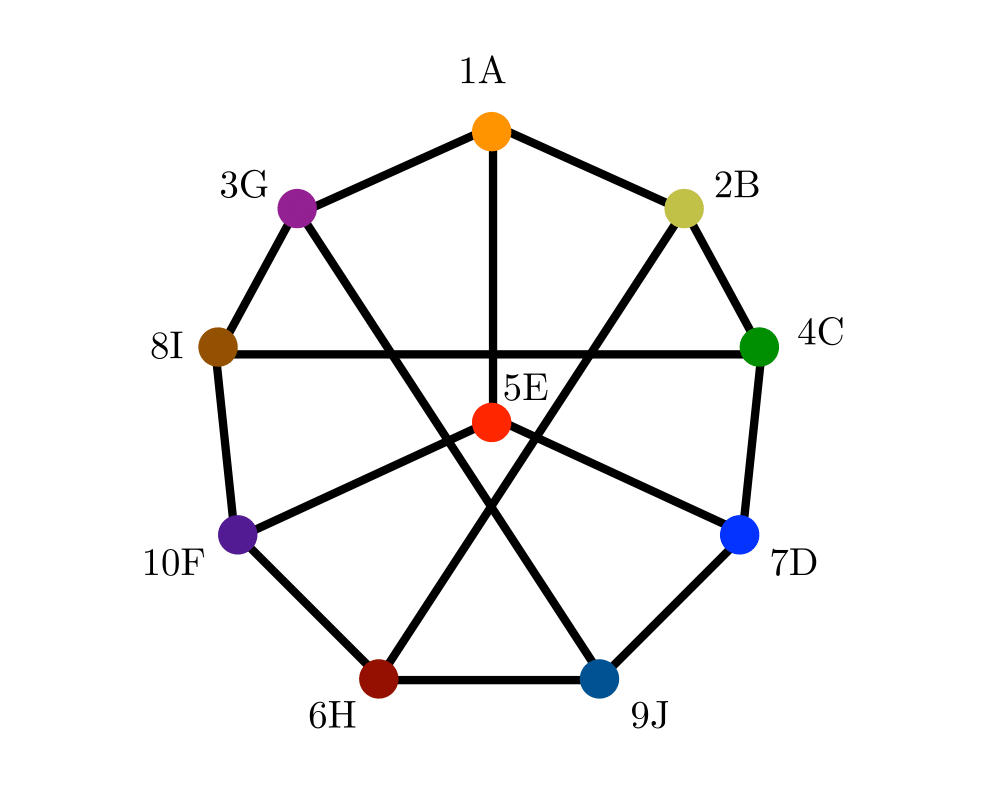  Graph Isomorphism |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
The Art of Computer Programming, Volume 4 Fascicle 4: Generating All Trees; History of Combinationatorial Generation by D. E. Knuth
Six Degrees: The Science of a Connected Age by Duncan J. Watts
Linked: The New Science of Networks by A. Barabasi
Random Graphs by B. Bollobas
Efficient Algorithms for Listing Combinatorial Structures by L. Goldberg
Graphical enumeration by F. Harary and E. Palmer