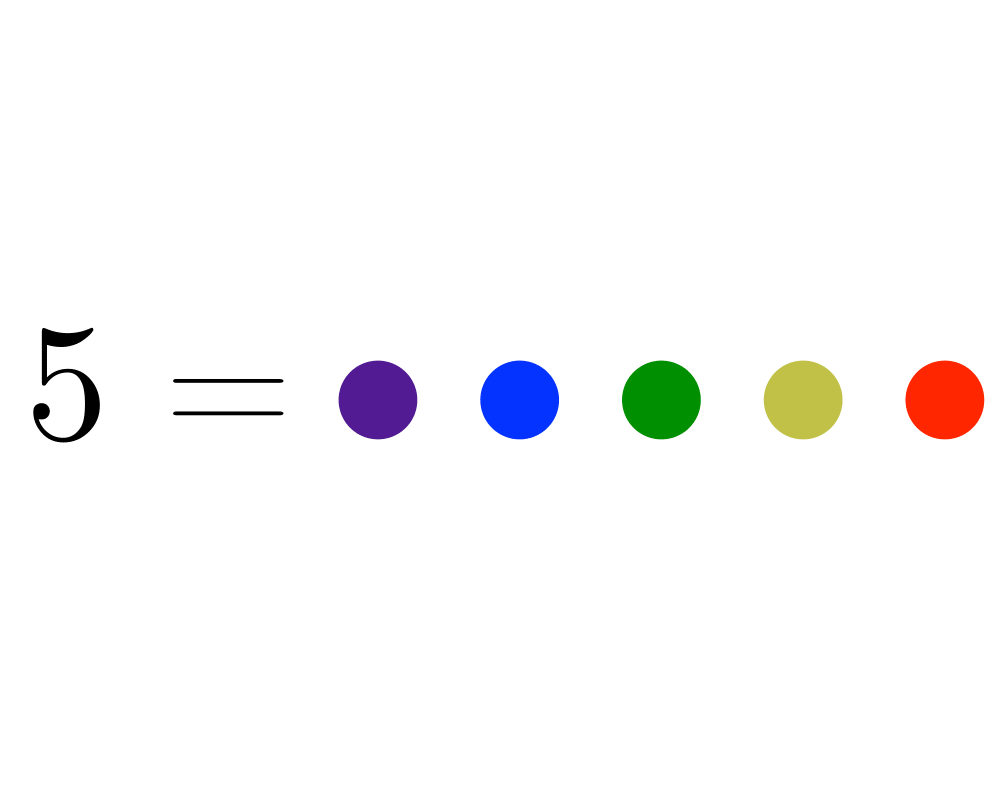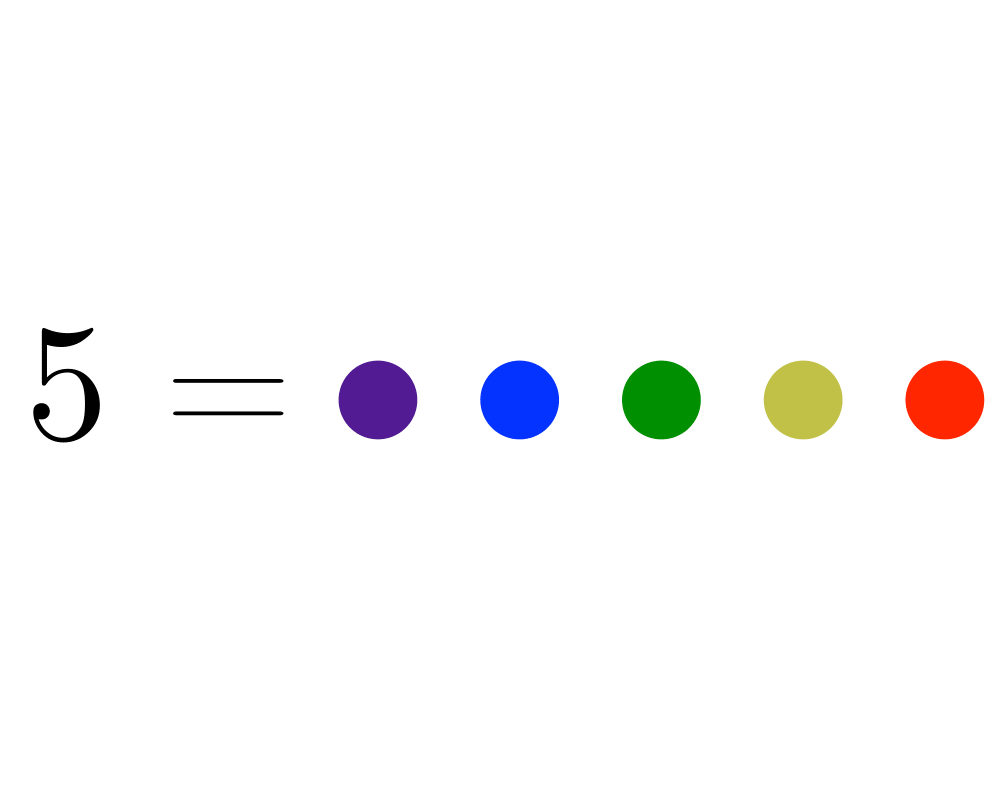Input

Output

Input Description: An integer \(n\).
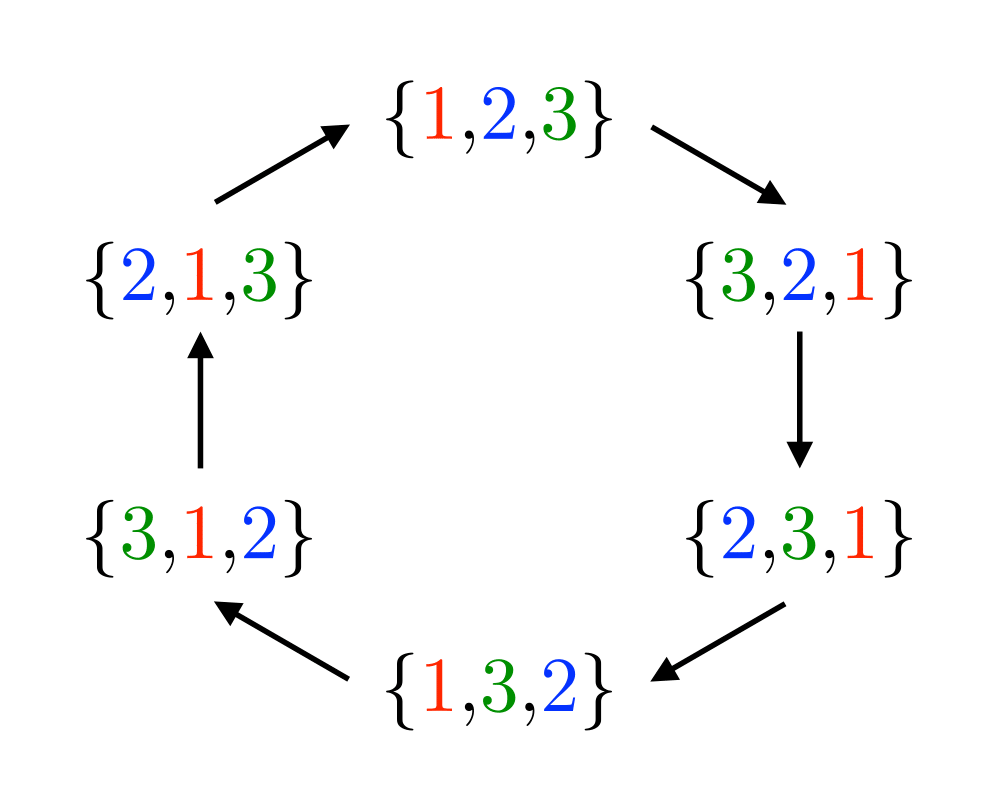
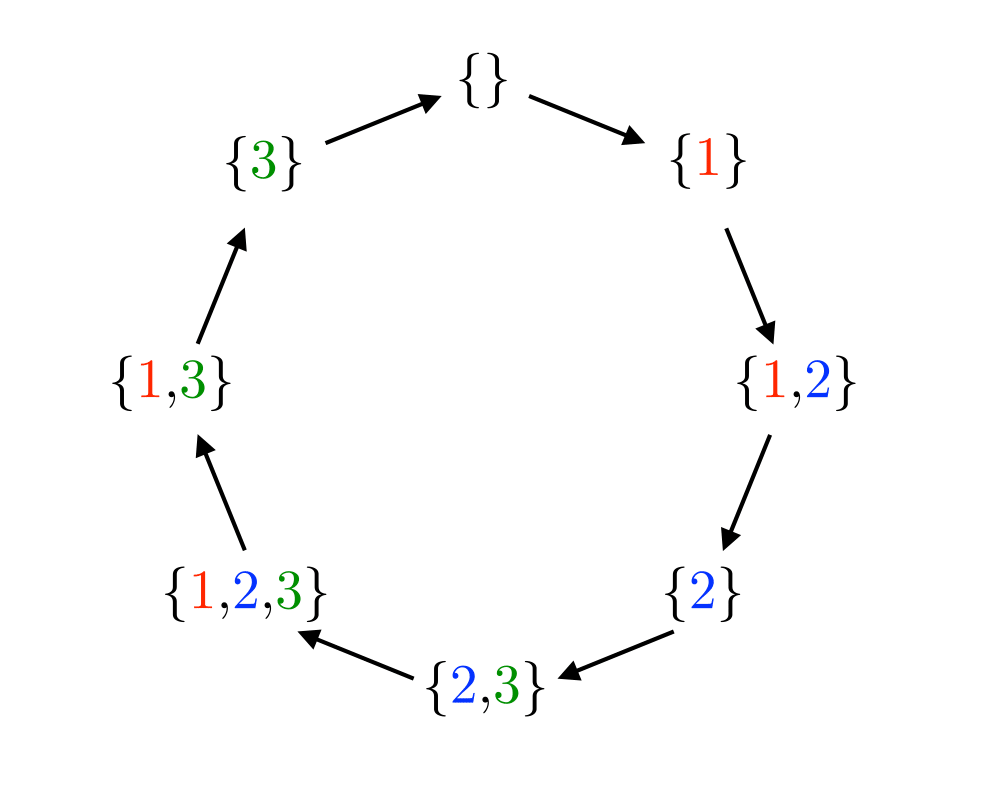
Problem: Generate (1) all, or (2) a random, or (3) the next integer or set partitions of length \(n\).

Excerpt from The Algorithm Design Manual: There are two different types of combinatorial objects denoted by the term ``partition'', namely integer partitions and set partitions. Although they are quite different beasts, it is a good idea to make both a part of your vocabulary:

• Integer partitions of \(n\) are sets of nonzero integers that add up to exactly \(n\). For example, the seven distinct integer partitions of 5 are {5}, {4,1}, {3,2}, {3,1,1}, {2,2,1}, {2,1,1,1}, and {1,1,1,1,1}. An interesting application I encountered that required the generation of integer partitions was in a simulation of nuclear fission. When an atom is smashed, the nucleus of protons and neutrons is broken into a set of smaller clusters. The sum of the particles in the set of clusters must equal the original size of the nucleus. As such, the integer partitions of this original size represent all the possible ways to smash the atom.
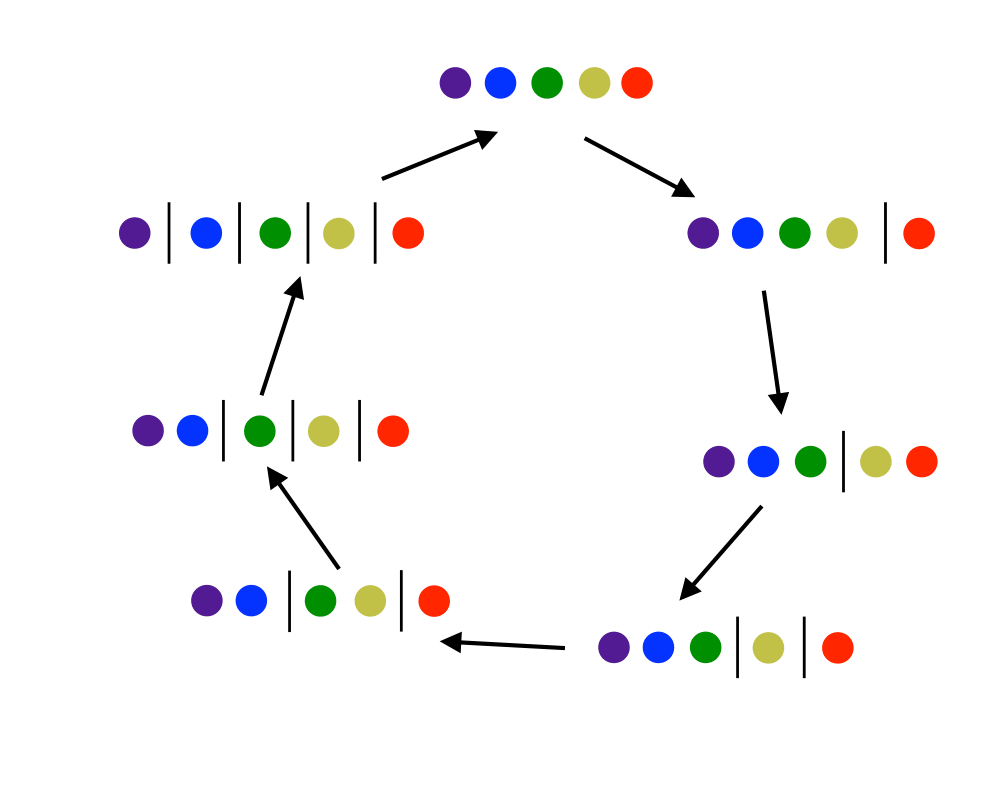
• Set partitions divide the elements \(1,\ldots,n\) into nonempty subsets. For example, there are fifteen distinct set partitions of \(n=4\): {1234}, {123,4}, {124,3},{12,34},{12,3,4},{134,2},{13,24},{13,2,4},{14,23},{1,234},{1,23,4},{14,2,3},{1,24,3}, {1,2,34}, and {1,2,3,4}. Several of the problems in this catalog return set partitions as results, such as vertex coloring and connected components.

Implementations

CAGES (rating 9)	Frank Ruskey's Combinatorial Generation Resources (rating 8)
Nijenhuis and Wilf (rating 8)	FFT (rating 8)
perfect-layout (rating 7)	linear-partition (rating 7)
ParMetis (rating 7)	Combinatorica (rating 7)

Recommended Books

The Art of Computer Programming, Volume 4 Fascicle 4: Generating All Trees; History of Combinationatorial Generation by D. E. Knuth

The Art of Computer Programming, Volume 4 Fascicle 3: Generating All Combinations and Partitions by D. E. Knuth

The Theory of Partitions by G. Andrews

Related Problems

Generating Permutations	Generating Subsets	Random Number Generation
Set Data Structures

As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.