 |
 |
 |
 |
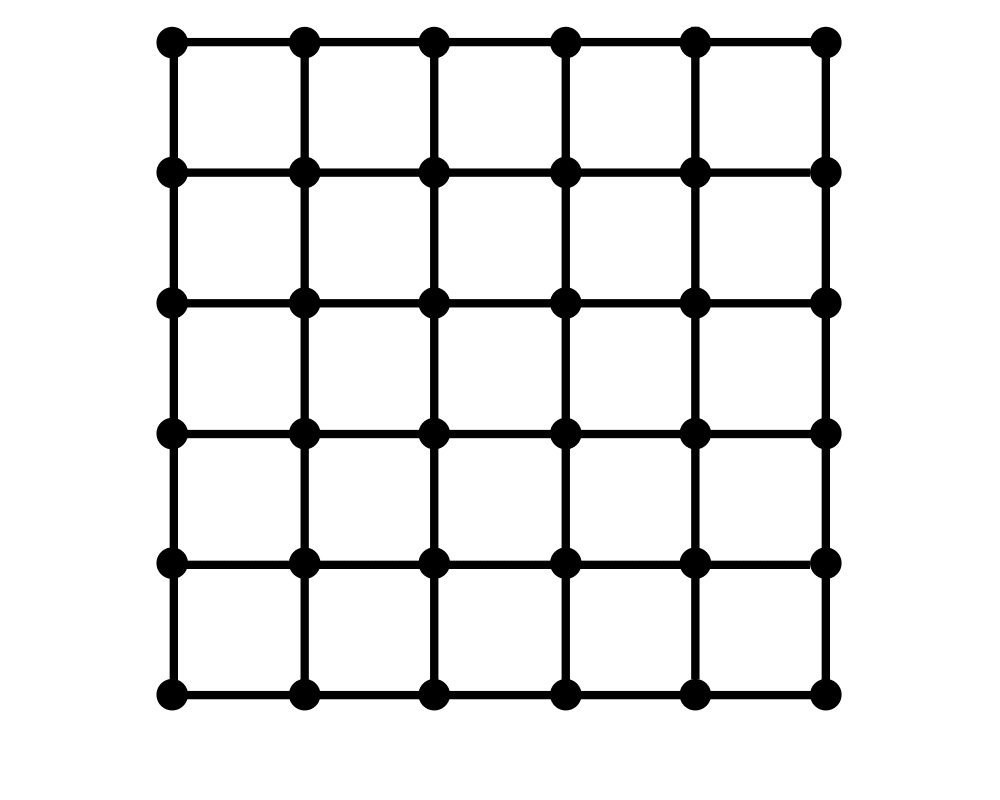
Input Description: A (weighted) graph \(G=(V,E)\). Integers \(j\), \(k\), and \(m\).
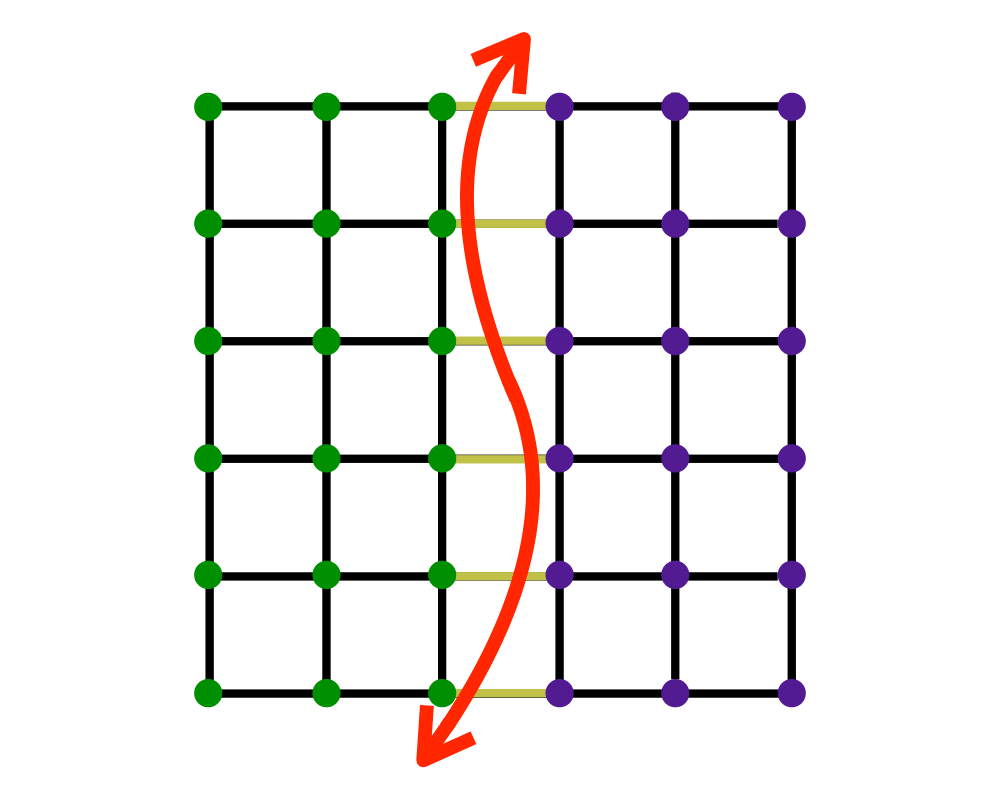
Problem: Partition the vertices into \(m\) subsets such that each subset has size at most \(j\), while the cost of the edges spanning subsets is bounded by \(k\).
Excerpt from The Algorithm Design Manual: Graph partitioning arises as a preprocessing step to divide-and-conquer algorithms, where it is often a good idea to break things into roughly equal-sized pieces. It also arises when dealing with extremely large graphs, when we need to cluster the vertices into logical components for storage (to improve virtual memory performance) or for drawing purposes (to collapse dense subgraphs into single nodes in order to reduce cluttering).
The basic approach to dealing with graph partitioning or max-cut problems is to construct an initial partition of the vertices (either randomly or according to some problem-specific strategy) and then sweep through the vertices, deciding whether the size of the cut would increase or decrease if we moved this vertex over to the other side. The decision to move \(v\) can be made in time proportional to its degree by simply counting whether more of \(v\)'s neighbors are on the same team as \(v\) or not. Of course, the desirable side for \(v\) will change if many of its neighbors jump, so multiple passes are likely to be needed before the process converges on a local optimum. Even such a local optimum can be arbitrarily far away from the global max-cut.
| Chaco (rating 10) |
SCOTCH (rating 9) |
| JOSTLE (rating 9) |
ParMetis (rating 9) |
| GOBLIN (rating 8) |
KaHIP (rating 7) |
| LINK (rating 5) |
 Spectral Graph Theory by F. Chung Spectral Graph Theory by F. Chung |
 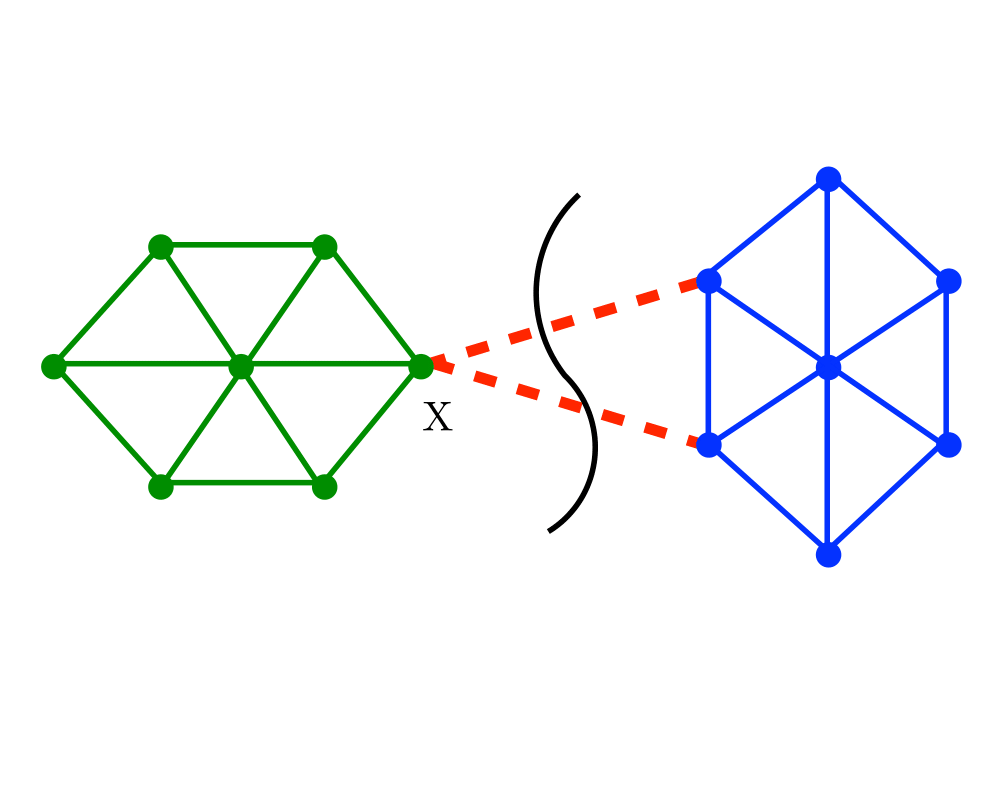 Edge and Vertex Connectivity |
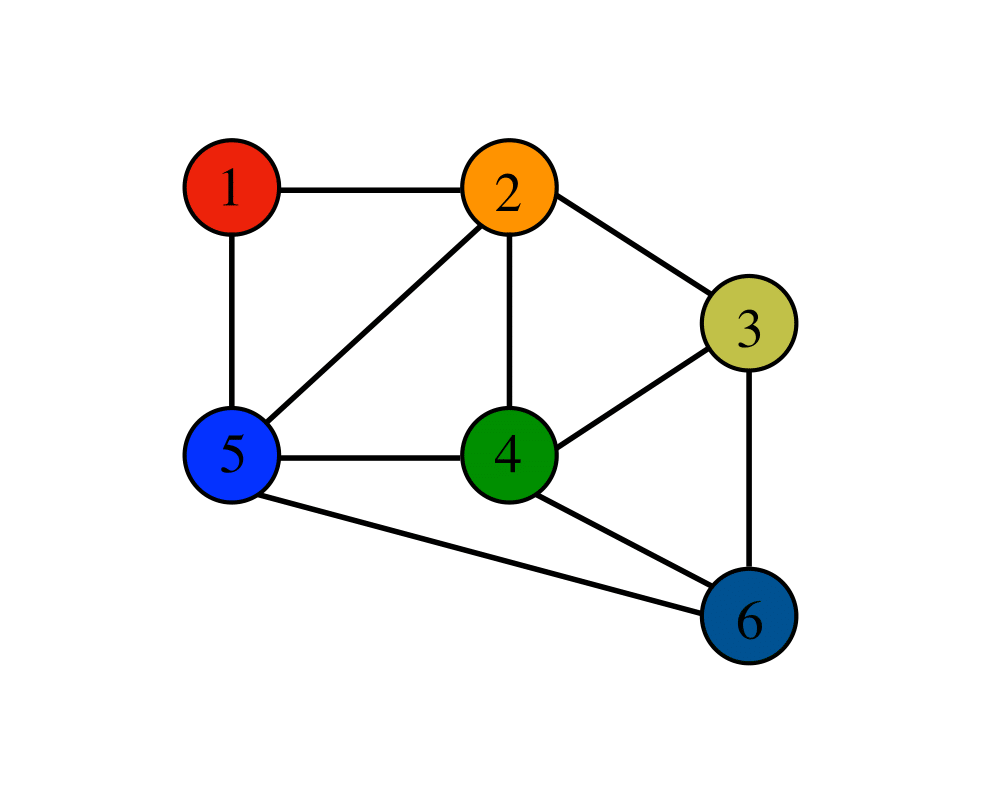 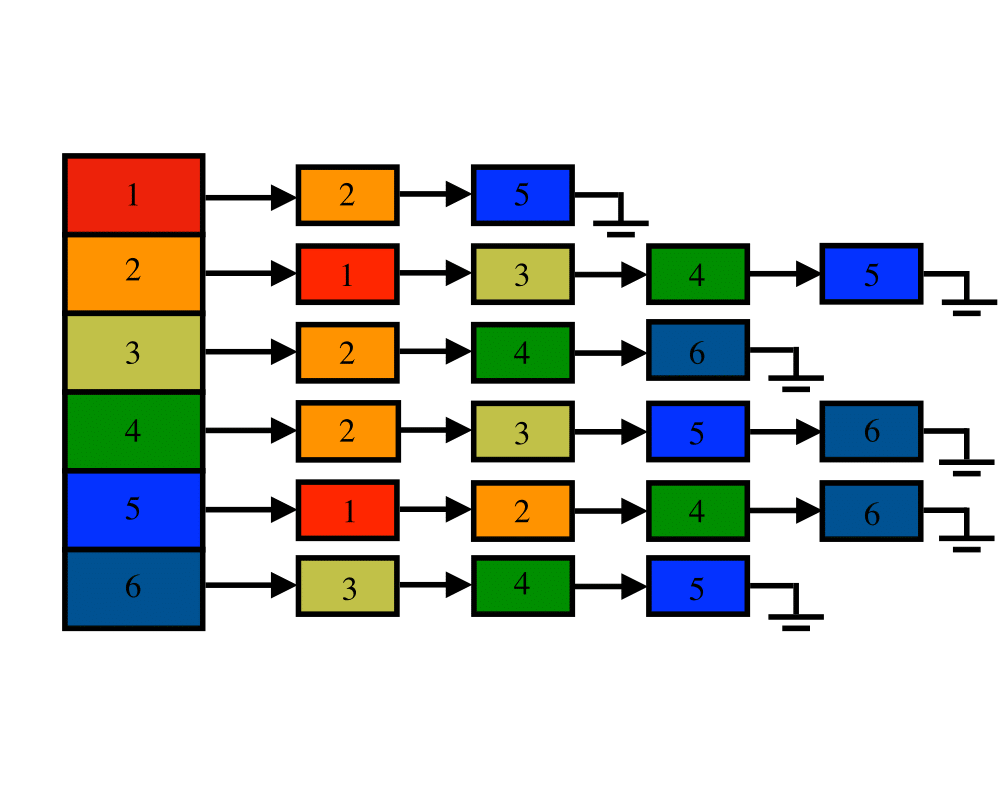 Graph Data Structures |
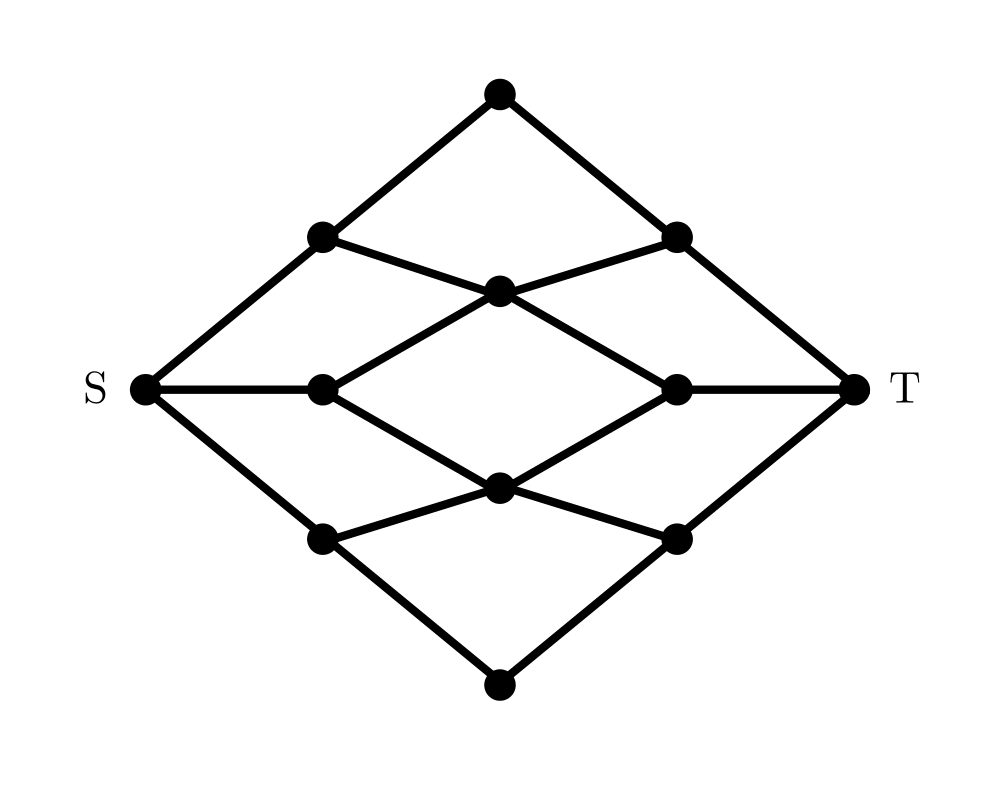 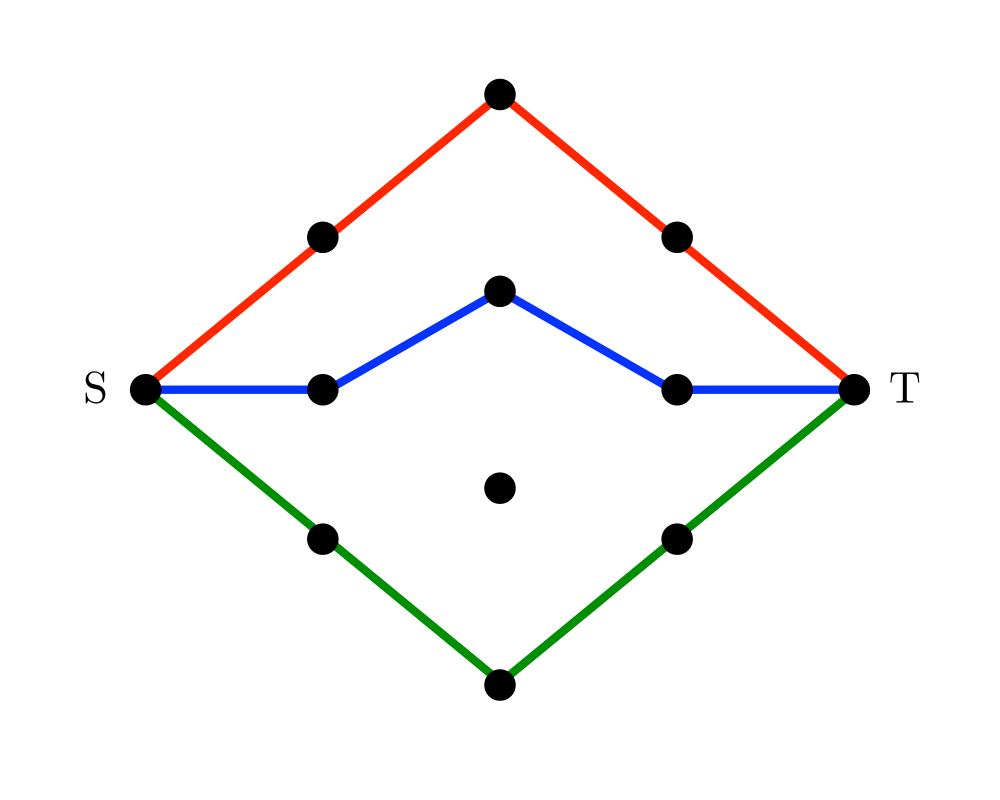 Network Flow |
  Planarity Detection and Embedding |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.