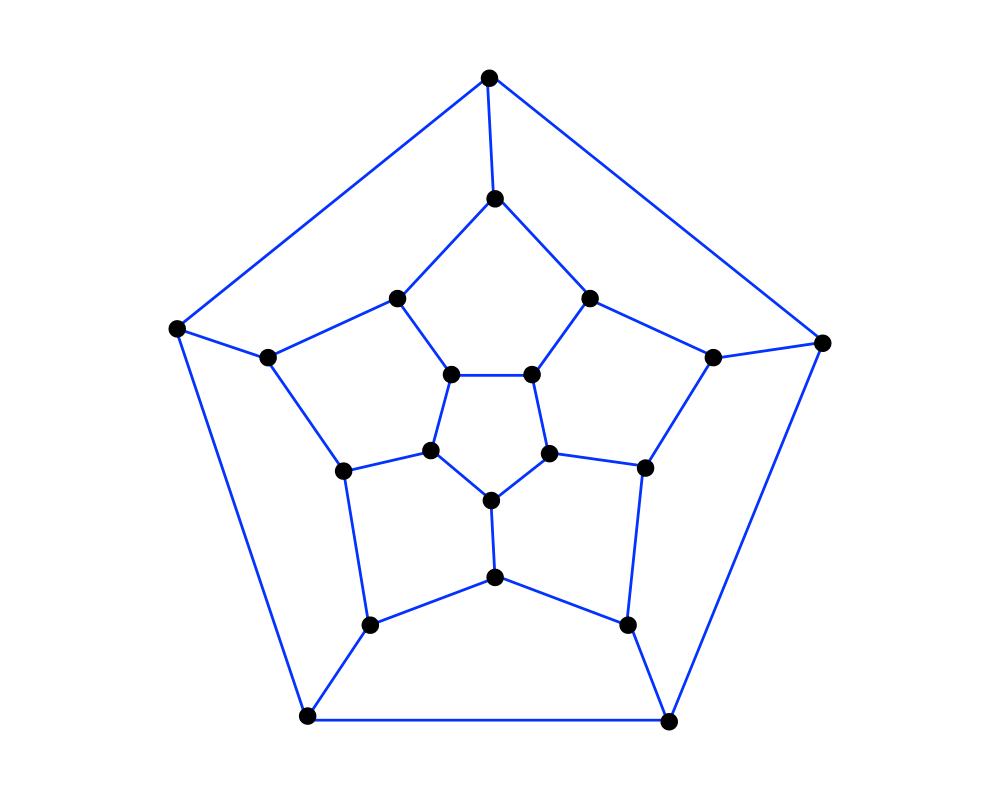
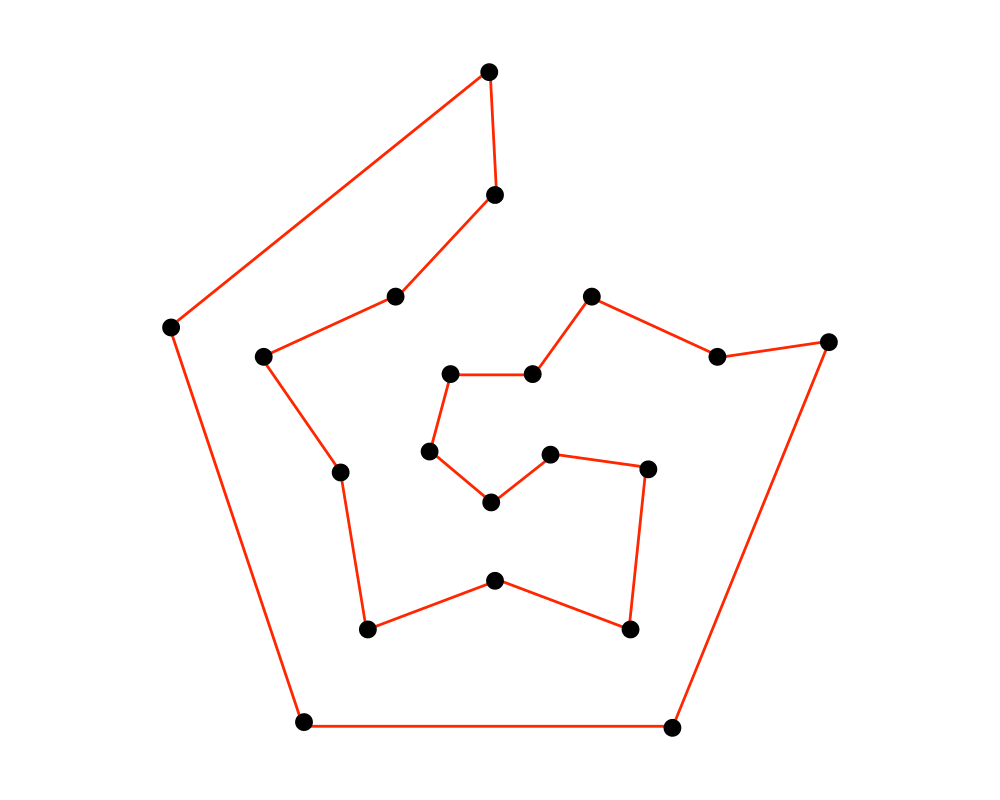
 |
 |
|
|
Input Description: A graph \(G = (V,E)\).
Problem: Find an ordering of the vertices such that each vertex is visited exactly once.
Excerpt from The Algorithm Design Manual: The problem of finding a Hamiltonian cycle or path in a graph is a special case of the traveling salesman problem, one where each pair of vertices with an edge between them has distance 1, while nonedge vertex pairs are separated by distance \(infinity\).
Closely related is the problem of finding the longest path or cycle in a graph, which occasionally arises in pattern recognition problems. Let the vertices in the graph correspond to possible symbols, and let edges link symbols that can possibly be next to each other. The longest path through this graph is likely the correct interpretation.
| Concorde (rating 10) |
Vandegriend's Finding Hamiltonian Cycles (rating 9) |
| TSPLIB4J (rating 5) |
planham (rating 5) |
| Netlib (rating 5) |
Stanford Graphbase (rating 5) |
| Nijenhuis and Wilf (rating 4) |
  Eulerian Cycle/Chinese Postman |
  Traveling Salesman Problem |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
The Traveling Salesman Problem and Its Variations by G. Gutin and A. Punnen
Introduction to Graph Theory by Douglas B. West
The Traveling Salesman Problem: A computational study by D. Applegate and R. Bixby and V. Chvatal and W. Cook
The Traveling Salesman Problem : A Guided Tour of Combinatorial Optimization by E.L. Lawler (Editor) and A. H. Rinnooy-Kan