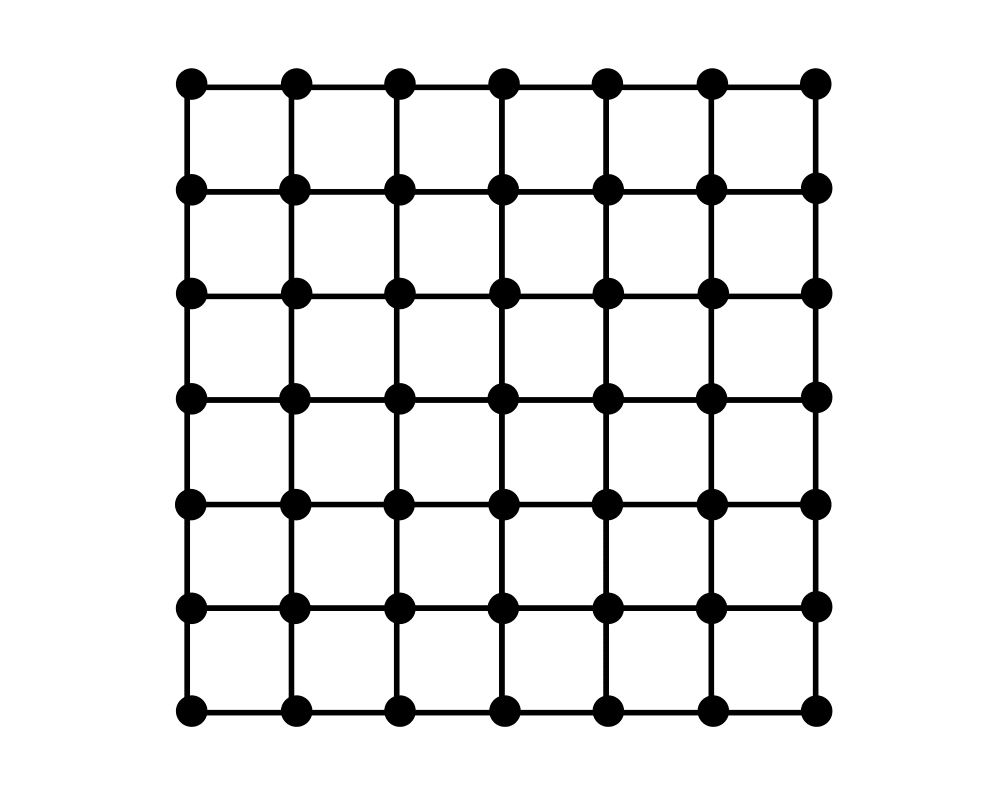
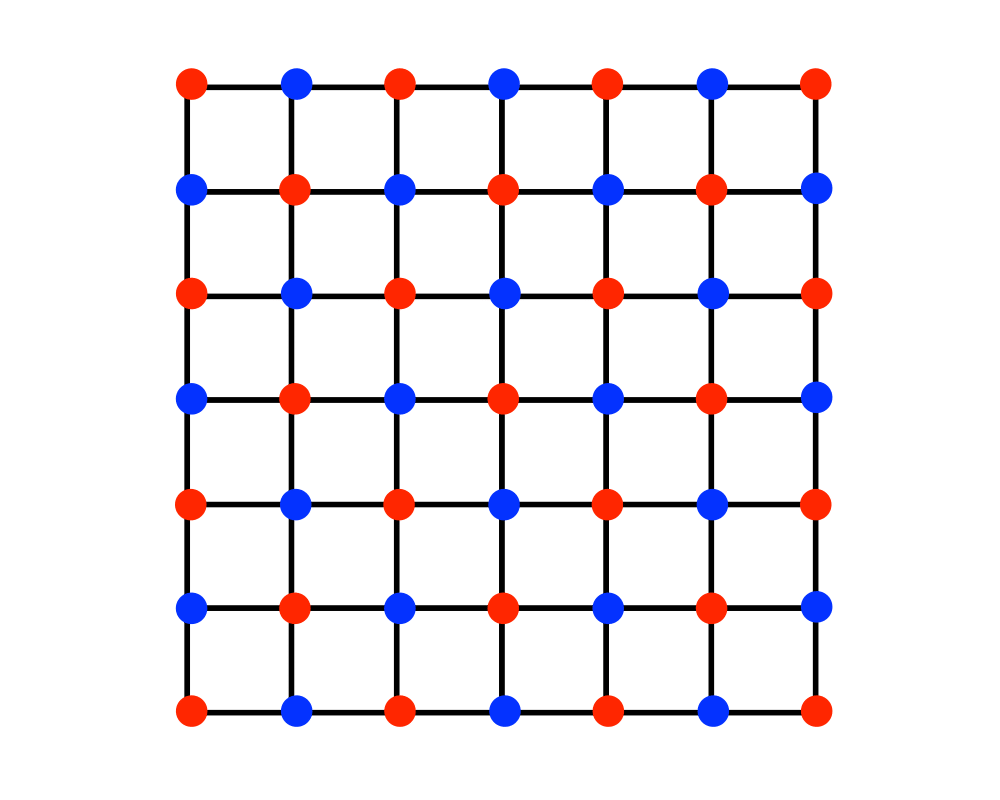
 |
 |
|
|
Input Description: A graph \(G=(V,E)\).
Problem: What is the largest subset of vertices of \(V\) such that no pair of vertices defines an edge of \(E\)?
Excerpt from The Algorithm Design Manual: The need to find large independent sets typically arises in dispersion problems, where we seek a set of mutually separated points. For example, suppose you are trying to identify locations for a new franchise service such that no two locations are close enough to compete with each other. Construct a graph where the vertices are possible locations, and add edges between any two locations deemed close enough to interfere. The maximum independent set gives you the maximum number of franchises you can sell without cannibalizing sales.
Independent sets avoid conflicts between elements and hence arise often in coding theory and scheduling problems. Define a graph whose vertices represent the set of possible code words, and add edges between any two code words sufficiently similar to be confused due to noise. The maximum independent set of this graph defines the highest capacity code for the given communication channel.
| GOBLIN (rating 9) |
GRASP (rating 8) |
| KaMIS (rating 5) |
MaxIndependentSet (rating 5) |
| Neural-Networks for Cliques and Coloring (rating 5) |
RAPID (rating 5) |
| GMT (rating 4) |
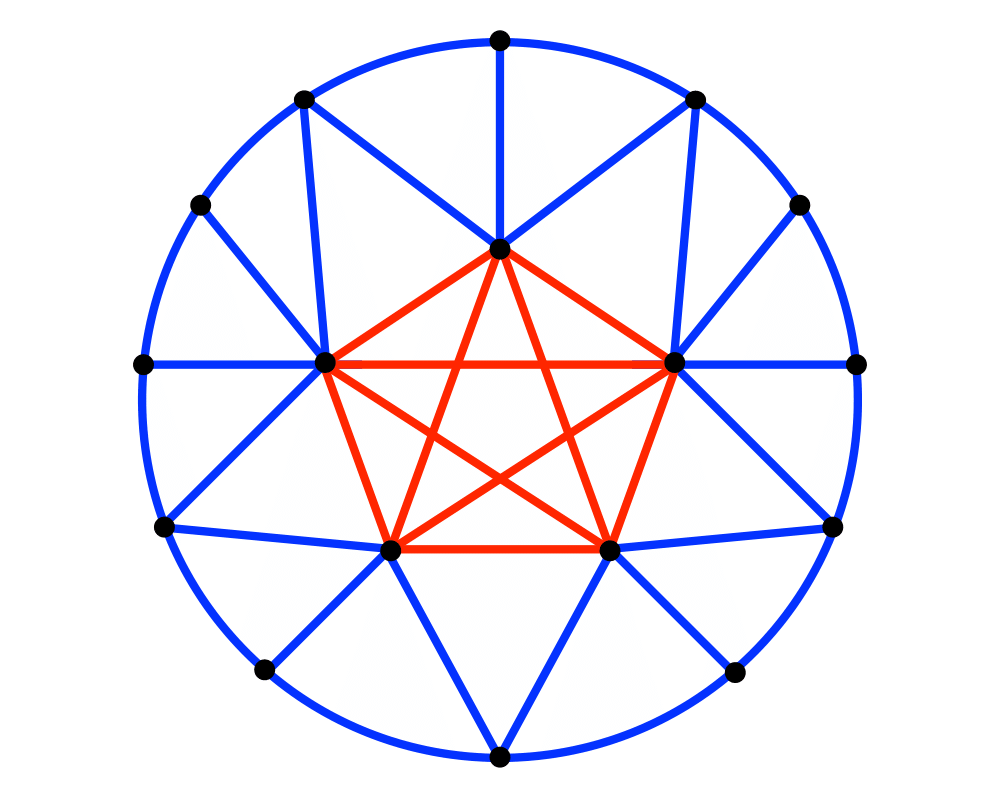  Clique |
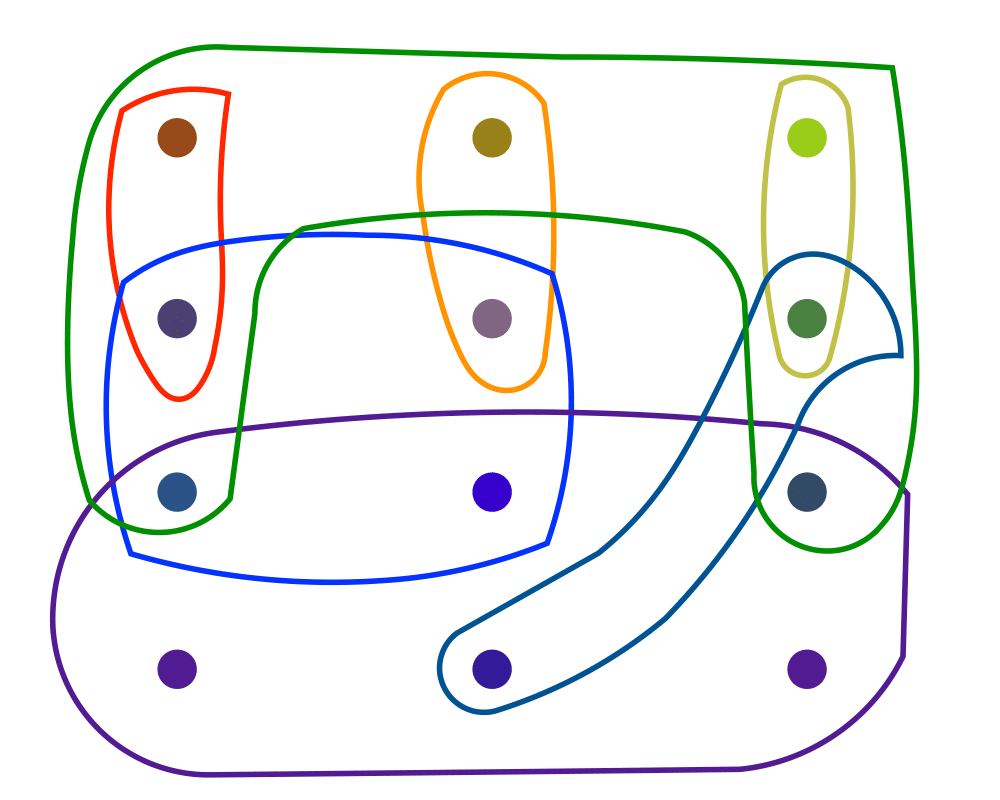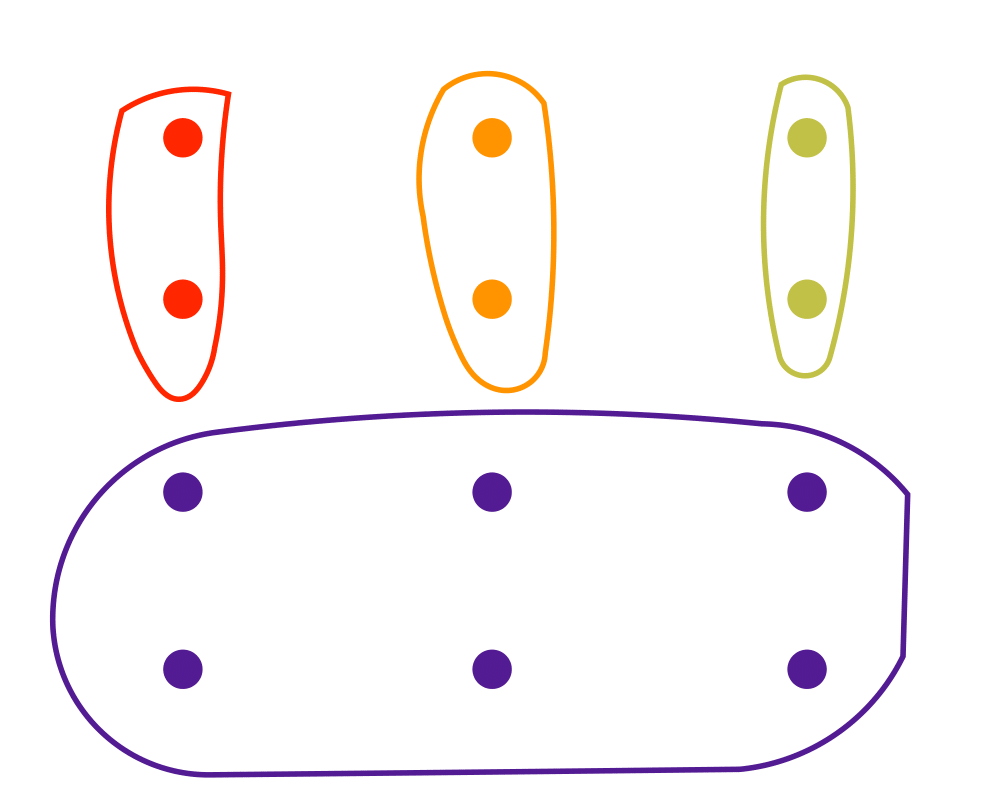  Set Packing |
  Vertex Coloring |
  Vertex Cover |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
Cliques, Coloring, and Satisfiability: Second Dimacs Implementation Challenge by David S. Johnson and Michael A. Trick, Editors
Computers and Intractability: A Guide to the Theory of NP-Completeness by M. R. Garey and D. S. Johnson
Combinatorial Optimization: Networks and Matroids by E. Lawler