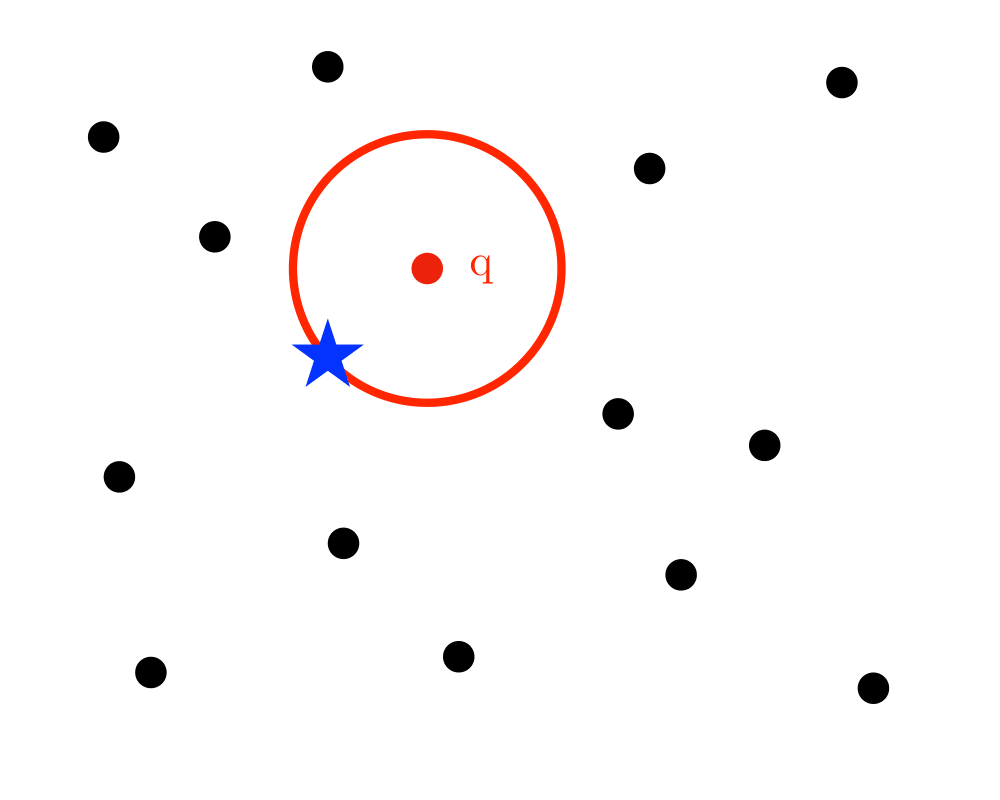
 |
 |
|
|
Input Description: A set \(S\) of \(n\) points in \(d\) dimensions; a query point \(q\).
Problem: Which point in \(S\) is closest to \(q\)?
Excerpt from The Algorithm Design Manual: The need to quickly find the nearest neighbor to a query point arises in a variety of geometric applications. The classic example in two dimensions is designing a system to dispatch emergency vehicles to the scene of a fire. Once the dispatcher learns the location of the fire, she uses a map to find the firehouse closest to this point so as to minimize transportation delays. This situation occurs in any application mapping customers to service providers.
Nearest-neighbor search is also important in classification. Suppose we are given a collection of data about people (say age, height, weight,years of education, sex, and income level) each of whom has been labeled as Democrat or Republican. We seek a classifier to decide which way a different person is likely to vote. Each of the people in our data set is represented by a party-labeled point in \(d\)-dimensional space. A simple classifier can be built by assigning to the new point the party affiliation of its nearest neighbor.
Such nearest-neighbor classifiers are widely used, often in high-dimensional spaces. The vector-quantization method of image compression partitions an image into \(8 X 8\) pixel regions. This method uses a predetermined library of several thousand \(8 X 8\) pixel tiles and replaces each image region by the most similar library tile. The most similar tile is the point in 64-dimensional space that is closest to the image region in question. Compression is achieved by reporting the identifier of the closest library tile instead of the 64 pixels, at some loss of image fidelity.
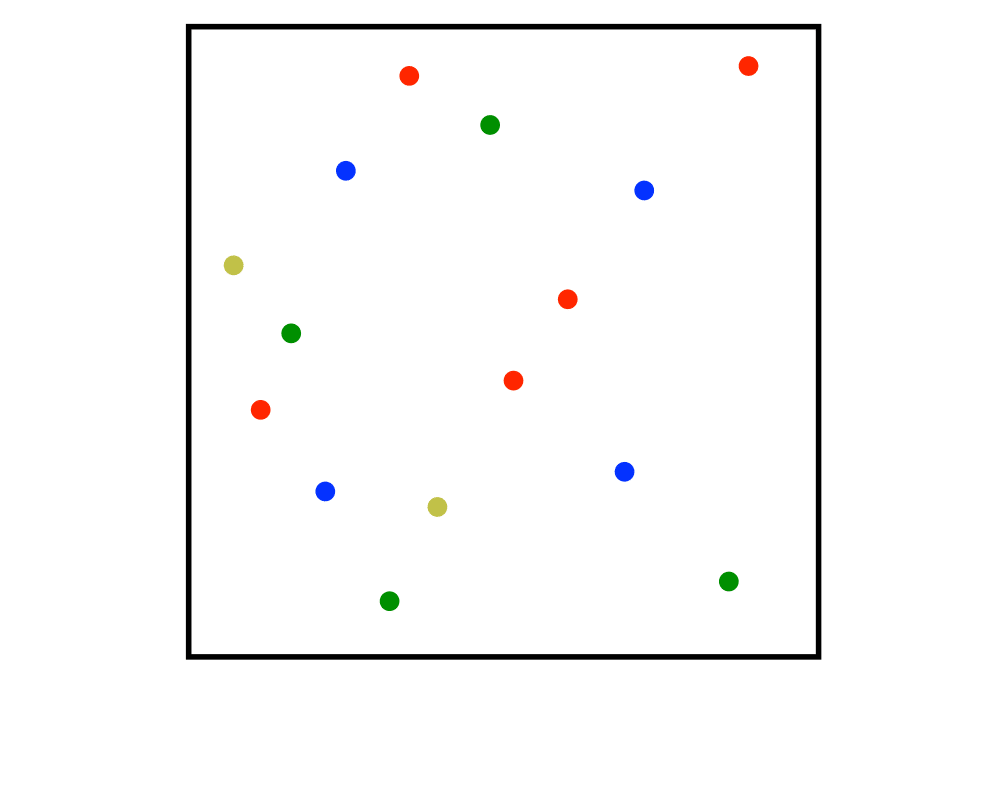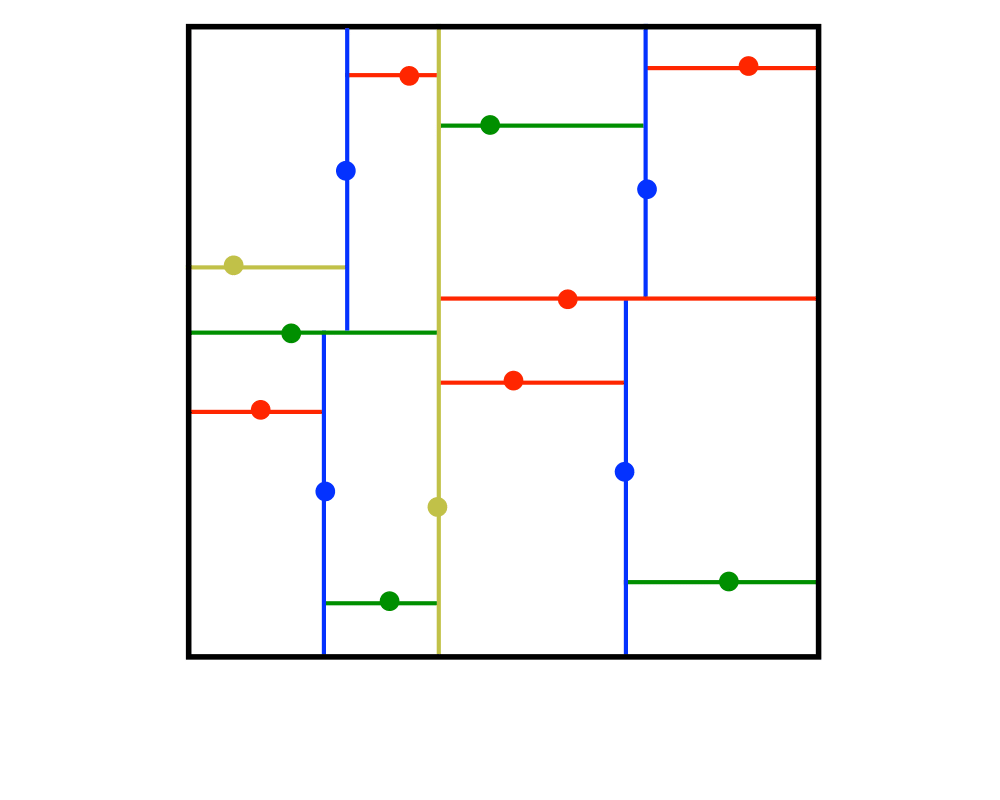  Kd-Trees |
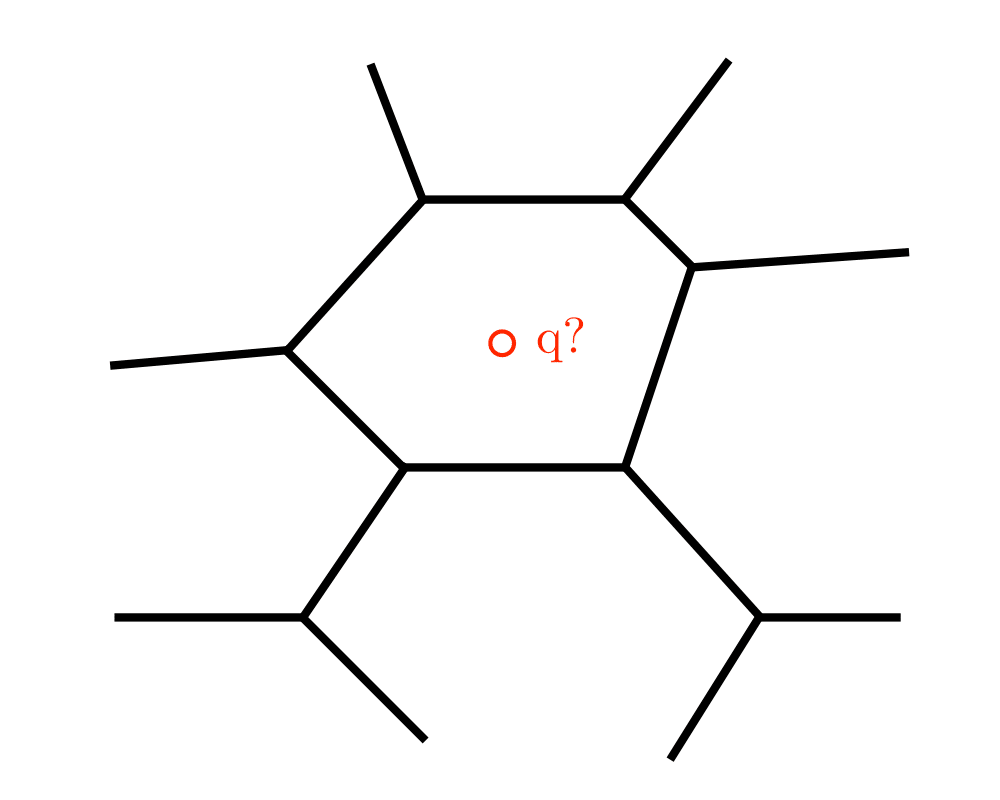  Point Location |
  Range Search |
  Voronoi Diagrams |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
Algorithms from P to NP, Vol. I: Design and Efficiency by B. Moret and H. Shapiro
Introduction to Algorithms by T. Cormen and C. Leiserson and R. Rivest and C. Stein
Applications of spatial data structures by H. Samet
The design and analysis of spatial data structures by H. Samet