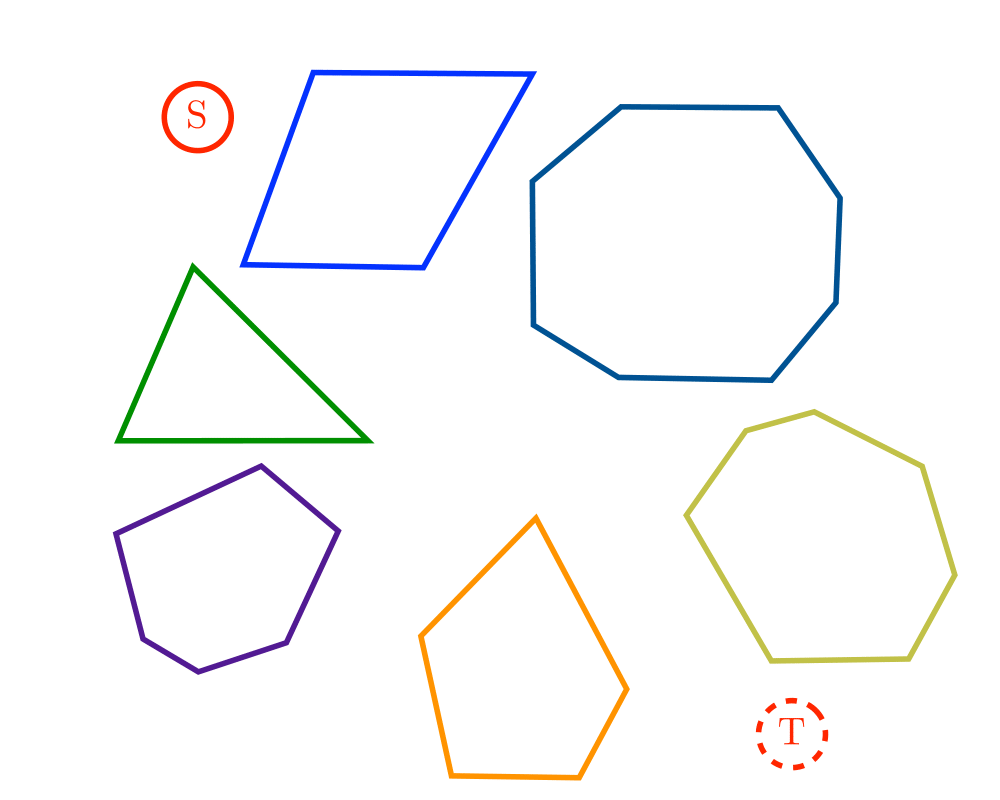
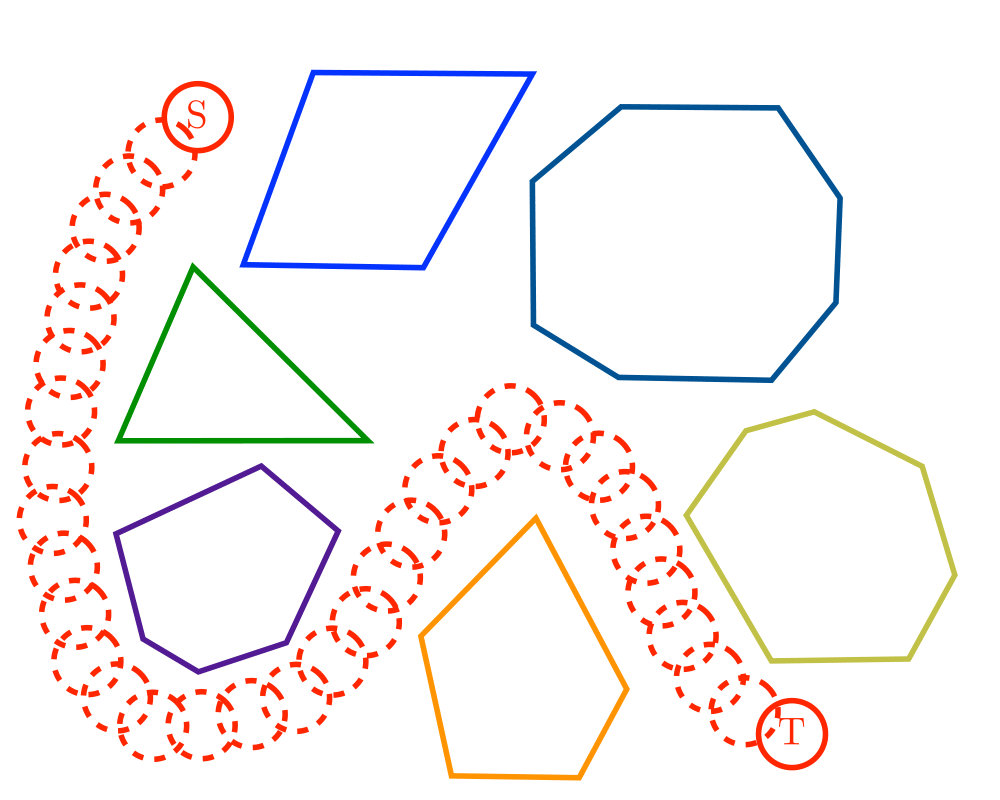
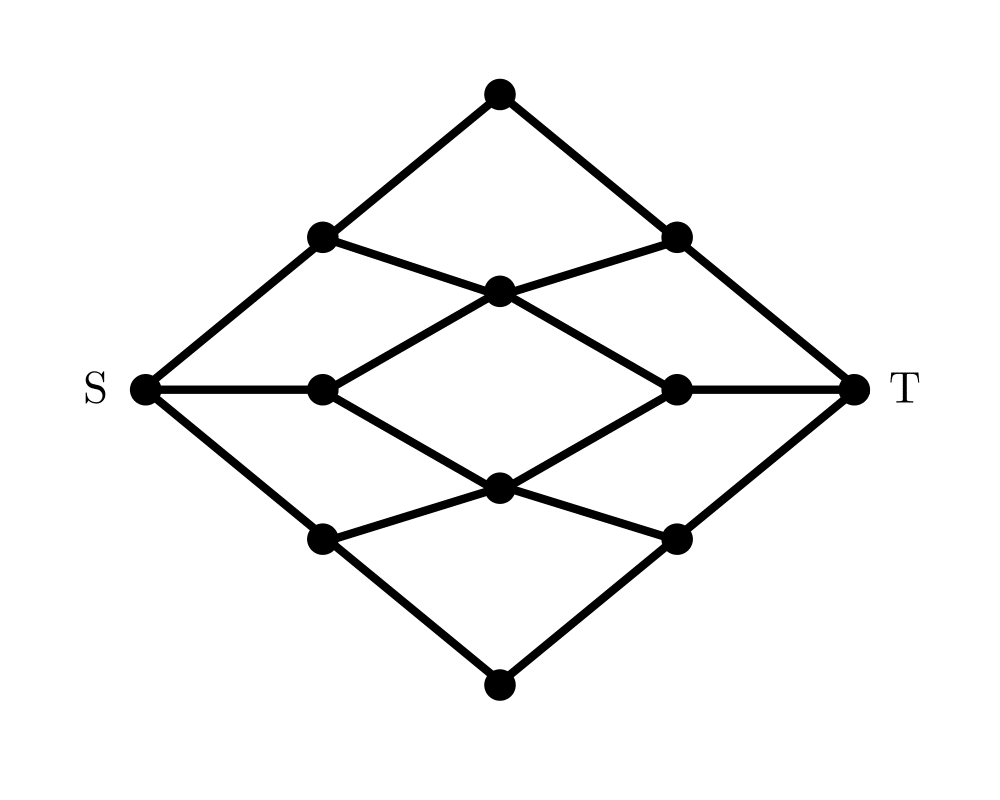
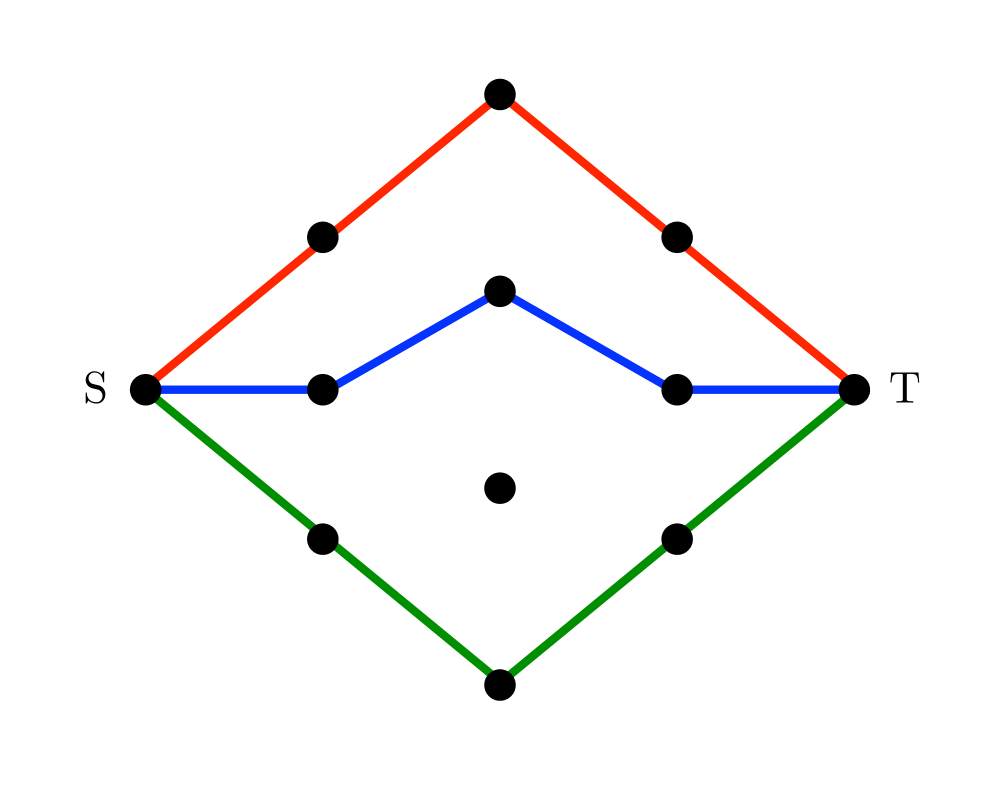
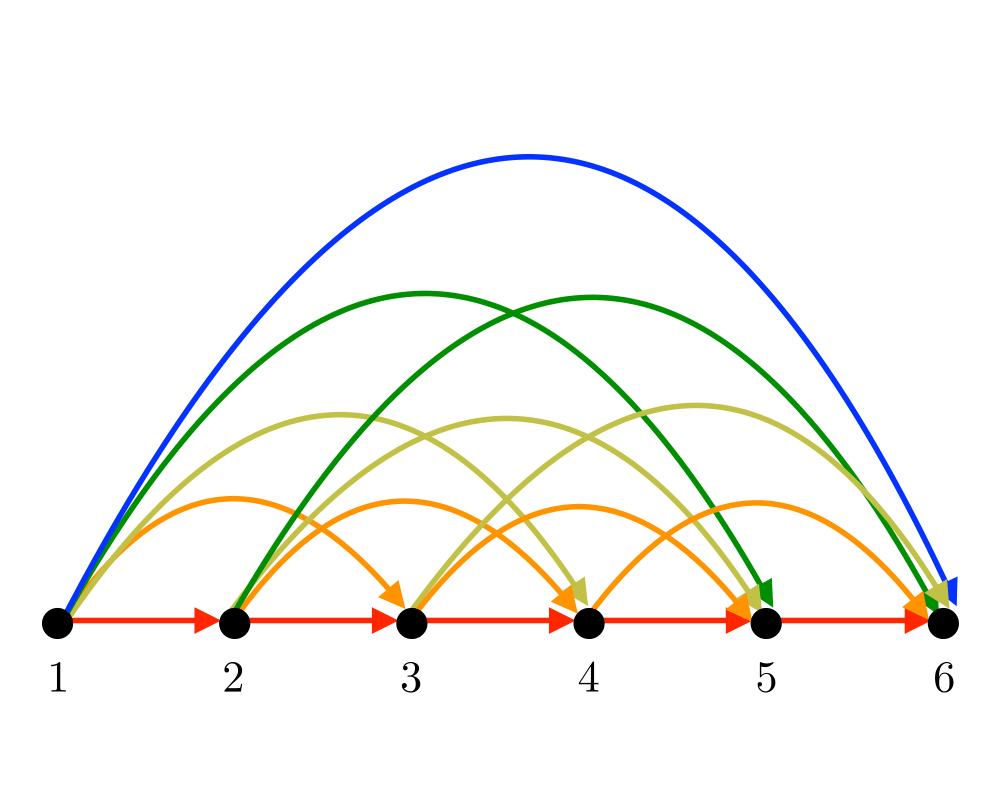
Input Description: An edge-weighted graph \(G\), with start vertex \(s\) and end vertex \(t\).
Problem: Find the shortest path from \(s\) to \(t\) in \(G\).
Excerpt from The Algorithm Design Manual: The problem of finding shortest paths in a graph has a surprising variety of applications:
- The most obvious applications arise in transportation or communications, such as finding the best route to drive between Chicago and Phoenix or figuring how to direct packets to a destination across a network.
- Consider the problem of image segmentation, that is, separating two characters in a scanned, bit-mapped image of printed text. We need to find the separating line between two points that cuts through the fewest number of black pixels. This grid of pixels can be modeled as a graph, with any edge across a black pixel given a high cost. The shortest path from top to bottom defines the best separation between left and right.
- A major problem in speech recognition is distinguishing between words that sound alike (homophones), such as to, two, and too. We can construct a graph whose vertices correspond to possible words, with an edge between possible neighboring words. If the weight of each edge measures the likelihood of transition, the shortest path across the graph defines the best interpretation of a sentence.
- Suppose we want to draw an informative picture of a graph. The center of the page should coorespond to the ``center'' of the graph, whatever that means. A good definition of the center is the vertex that minimizes the maximum distance to any other vertex in the graph. Finding this center point requires knowing the distance (i.e. shortest path) between all pairs of vertices.
Implementations
Recommended Books
Related Problems
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
Go To Main Page
The Boost Graph Library: user guide and reference manual by J. Siek and L. Lee and A. Lumsdaine
Network Flows : Theory, Algorithms, and Applications by Ravindra K. Ahuja, Thomas L. Magnanti, and James B. Orlin