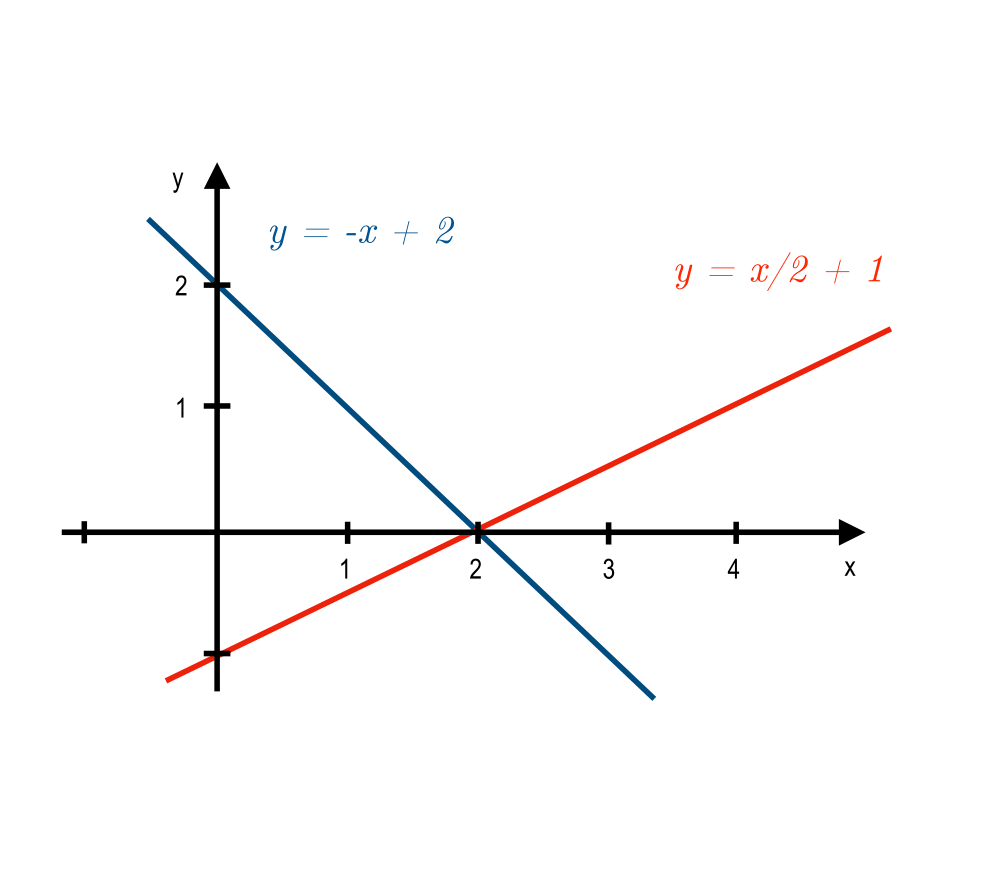 |
 |
 |
 |
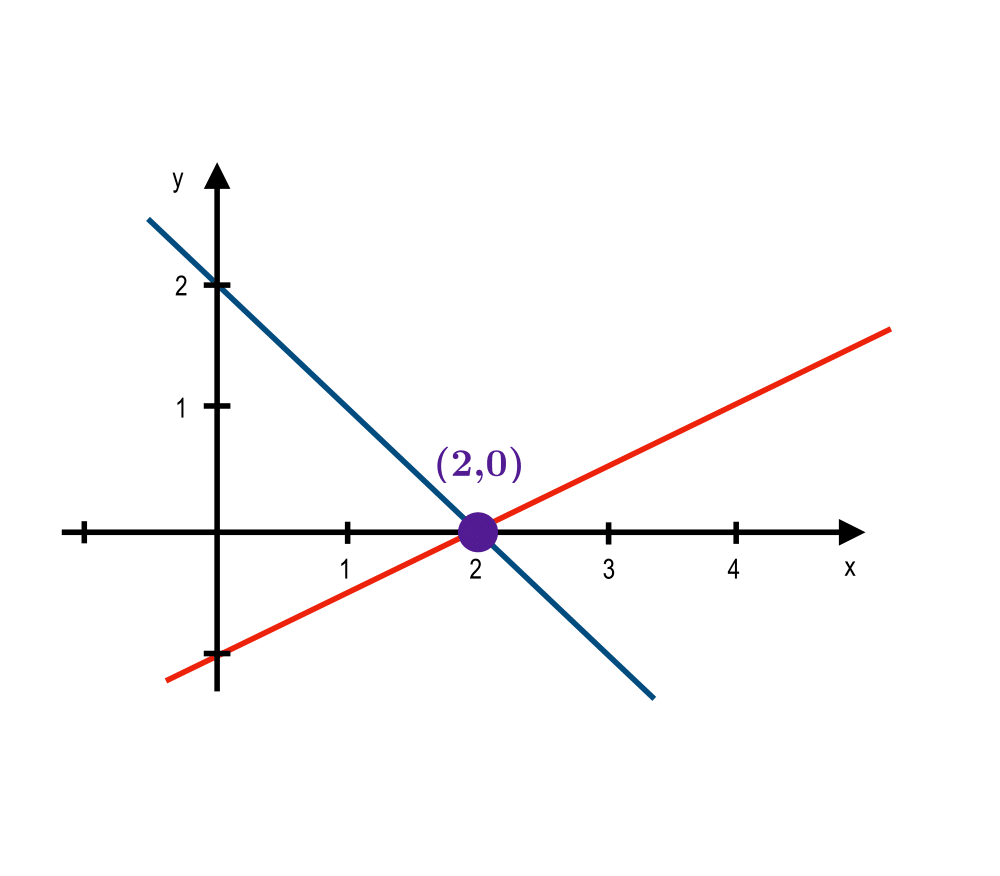
Input Description: An \(m x n\) matrix \(A\), and an \(m x 1\) vector \(b\), representing \(m\) linear equations with \(n\) variables.
Problem: What is the vector \(x\) such that \(A \cdot x = b\)?
Excerpt from The Algorithm Design Manual: Solving linear systems is a problem of such scientific and commercial importance that excellent codes are readily available. There is likely no good reason to implement your own solver, even though the basic algorithm (Gaussian elimination) is one we learned in high school. This is especially true if you are working with large systems.
Gaussian elimination is based on the fact that the solution to a system of linear equations is invariant under scaling (multiplying both sides by a constant; i.e. if \(x=y\), then \(2x=2y\)) and adding equations (i.e. the solution to the equations \(x=y\) and \(w=z\) is the same as the solution to \(x=y\) and \(x+w=y+z\)). Gaussian elimination scales and adds equations so as to eliminate each variable from all but one equation, leaving the system in such a state that the solution can just be read off from the equations.
| LAPACK (rating 10) |
LAPACK++ (rating 10) |
| JScience (rating 9) |
gosl (rating 8) |
| cudamat (rating 8) |
jblas (rating 8) |
| Elemental (rating 8) |
JAMA (rating 8) |
| Numerical Recipes (rating 8) |
 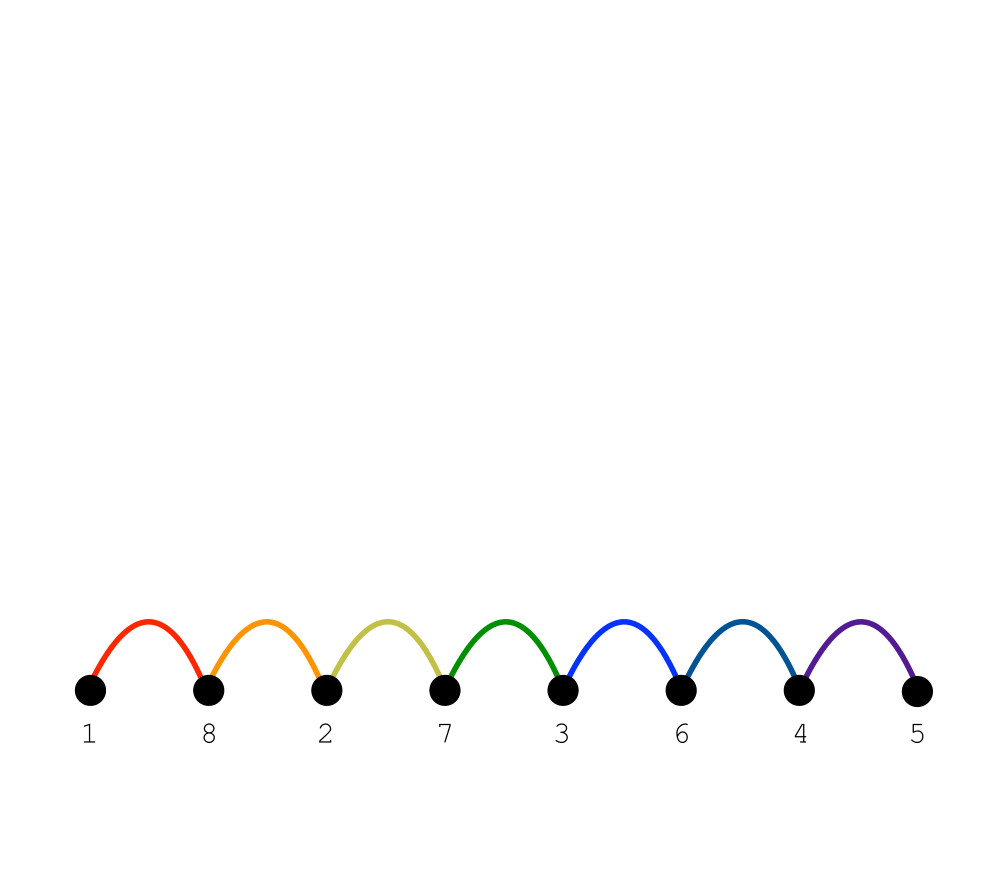 Bandwidth Reduction |
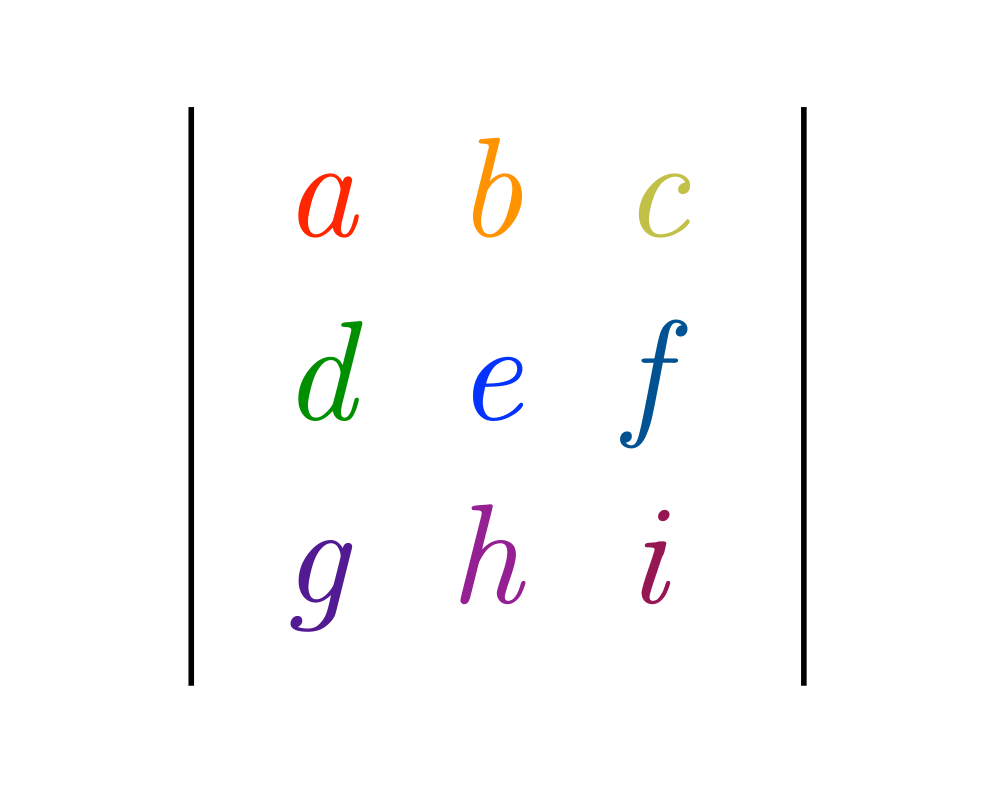 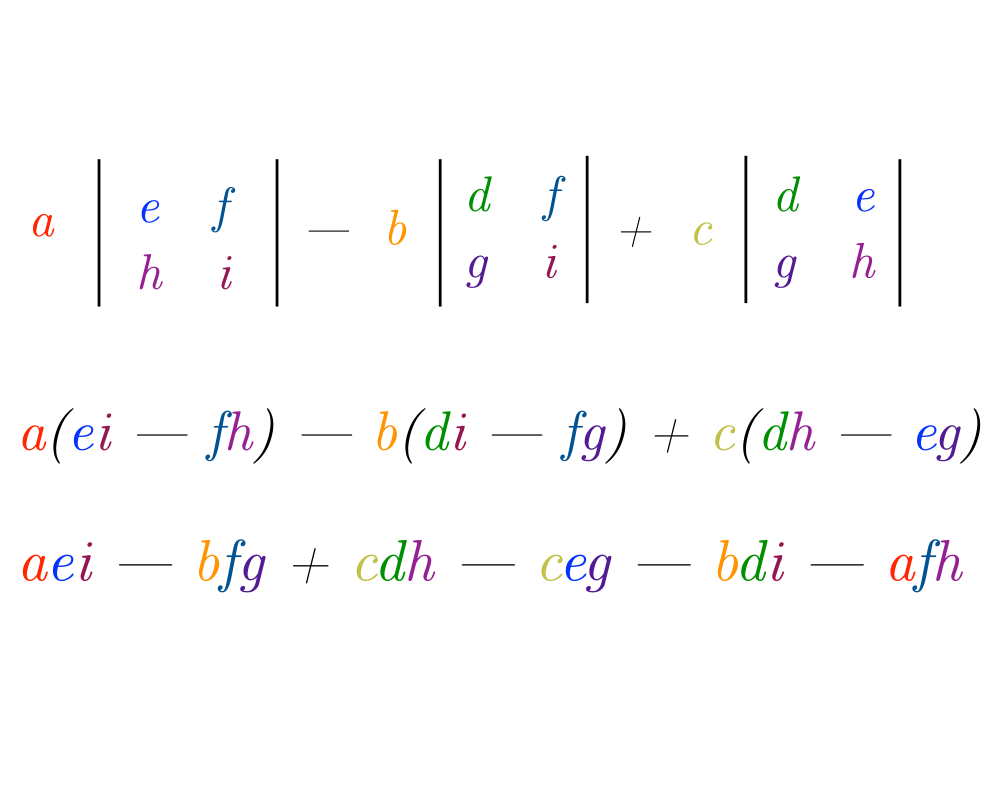 Determinants and Permanents |
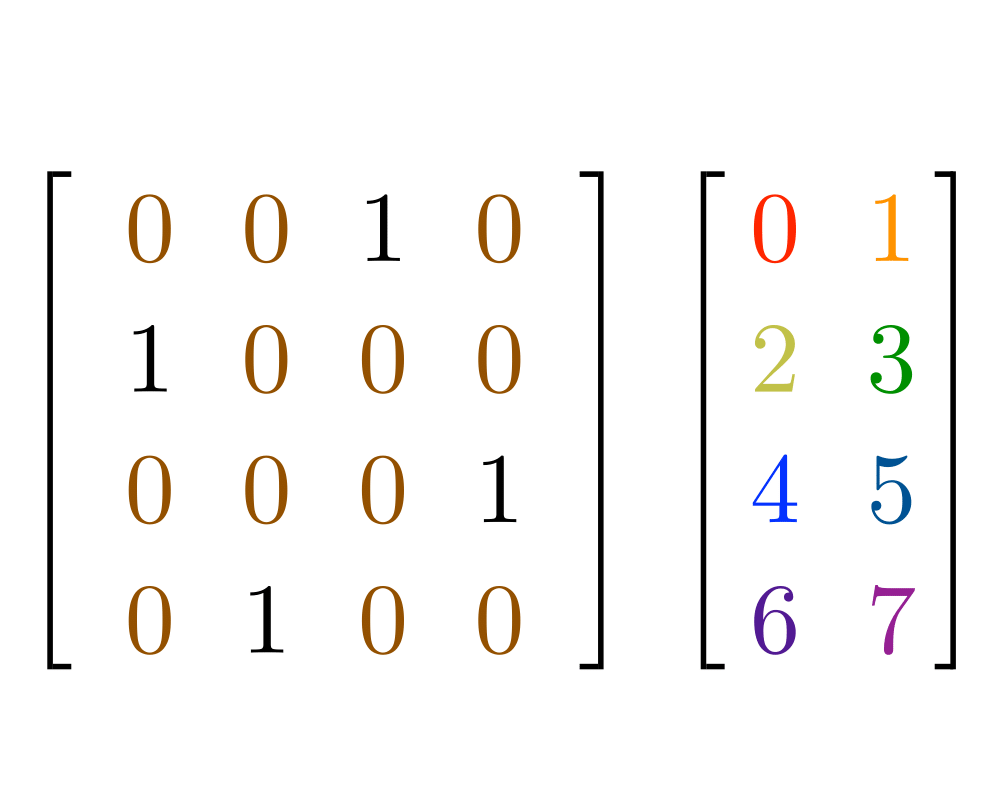  Matrix Multiplication |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.