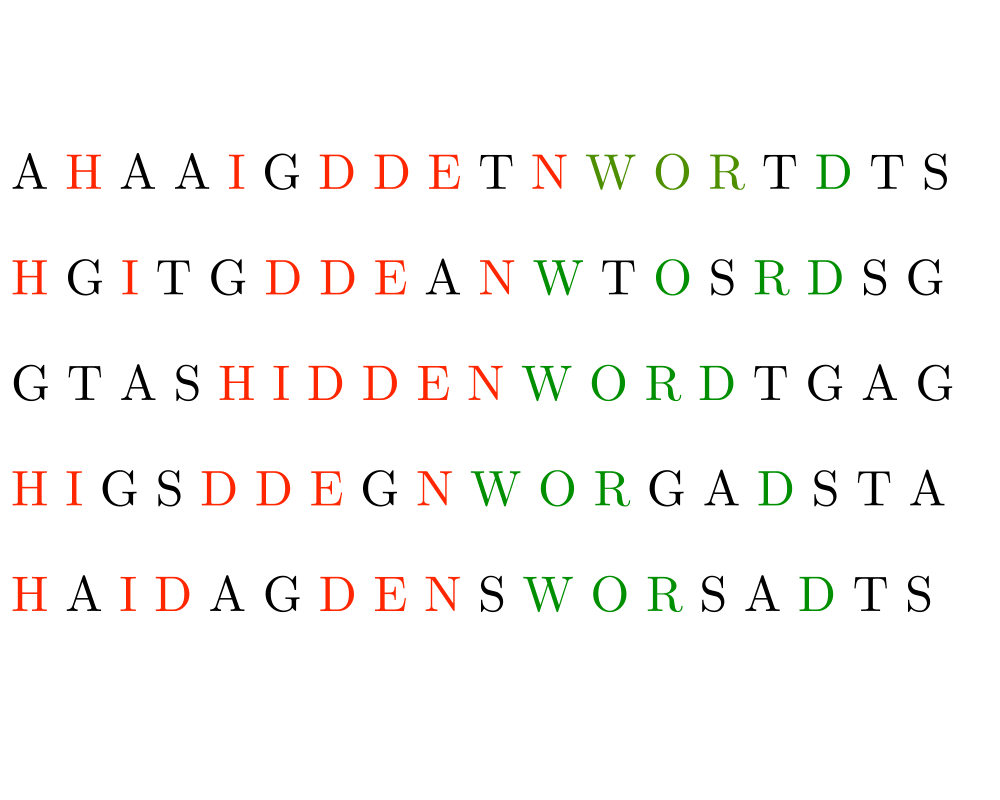 |
 |
|
|
Input Description: A set \(S\) of strings \(S_1,...,S_n\).
Problem: What is the longest string \(c\) such that for each \(S_i\), \(1 \leq i \leq n\), the characters of \(c\) appear as a scattered subsequence of \(S_i\)?
Excerpt from The Algorithm Design Manual: The problem of longest common subsequence arises whenever we search for similarities across multiple texts. A particularly important application is in finding a consensus among DNA sequences. The genes for building particular proteins evolve with time, but the functional regions must remain consistent in order to work correctly. By finding the longest common subsequence of the same gene in different species, we learn what has been conserved over time.
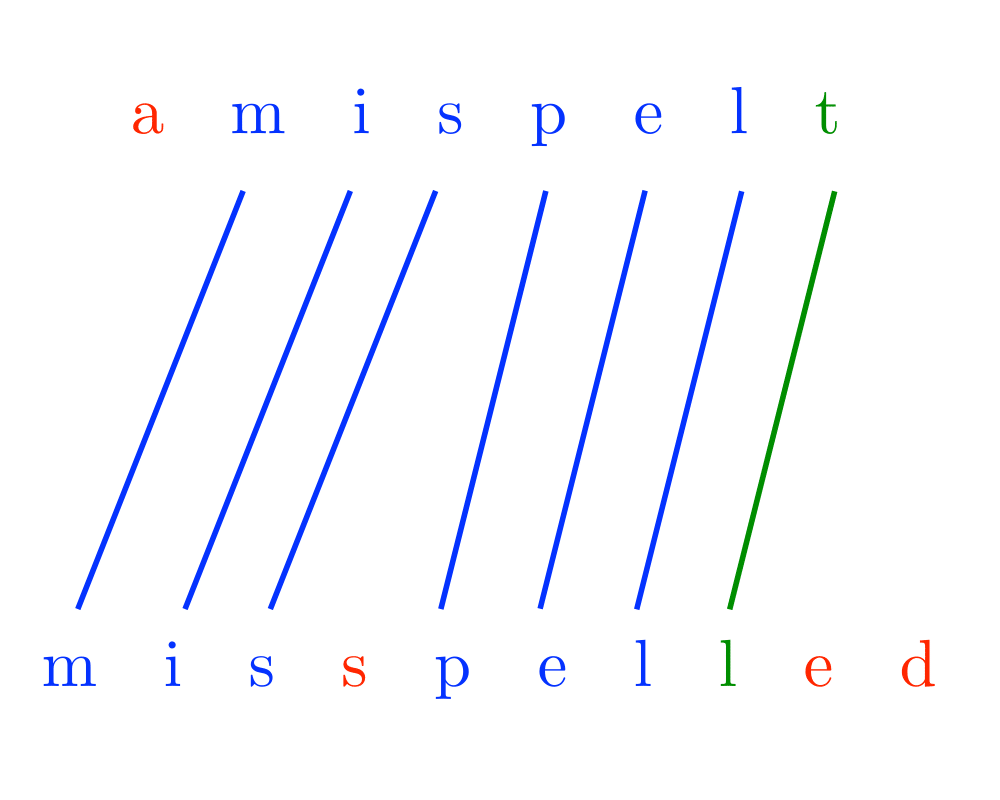
The longest common substring problem is a special case of edit distance, when substitutions are forbidden and only exact character match, insert, and delete are allowable edit operations. Under these conditions, the edit distance between \(p\) and \(t\) is \(n+m-2 |lcs(p,t)|\), since we can delete the missing characters from \(p\) to the \(lcs(p,t)\) and insert the missing characters from \(t\) to transform \(p\) to \(t\). This is particularly interesting because the longest common subsequence can be faster to compute than edit distance.
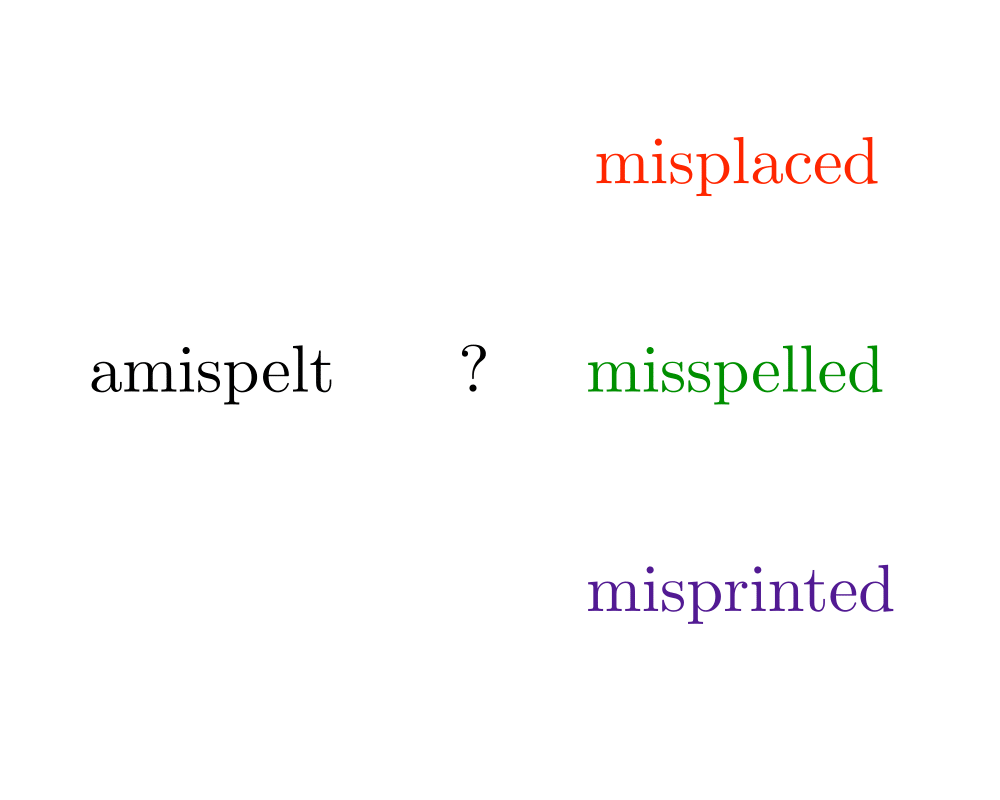  Approximate String Matching |
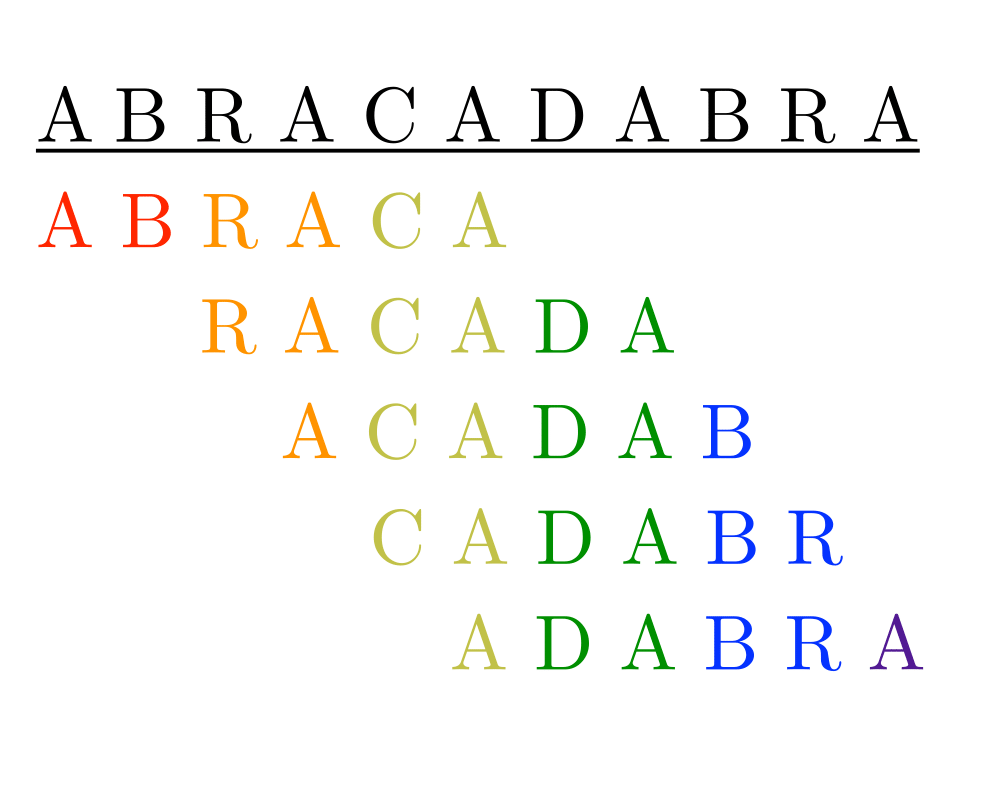  Shortest Common Superstring |
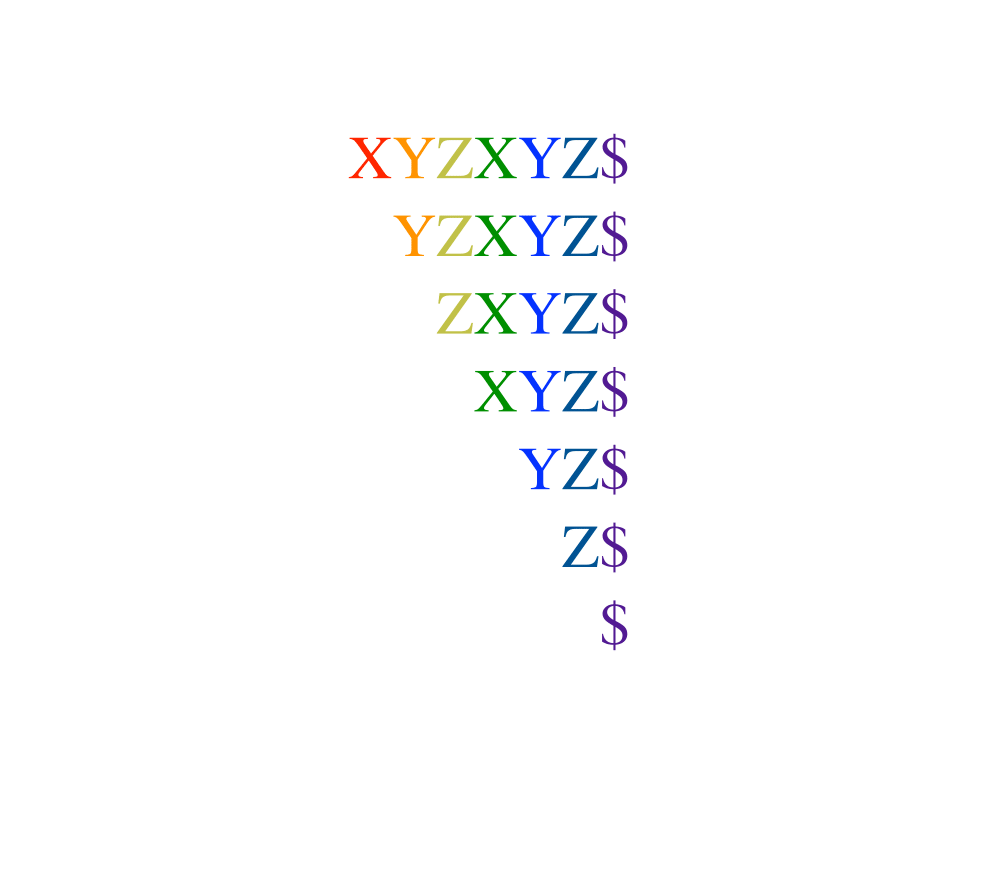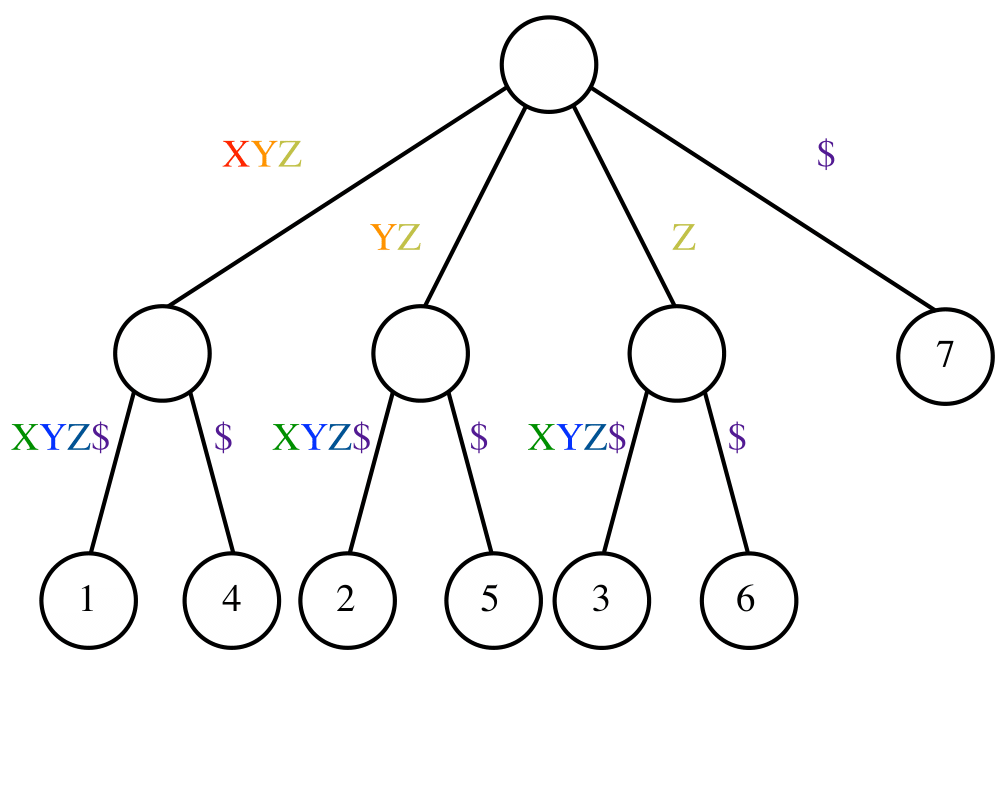  Suffix Trees and Arrays |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.
Algorithms on Strings, Trees, and Sequences by Dan Gusfield
Introduction to Computational Biology by M. Waterman
Handbook of Algorithms and Data Structures by G. Gonnet and R. Baeza-Yates
Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica by S. Pemmaraju and S. Skiena
Introduction to Algorithms by T. Cormen and C. Leiserson and R. Rivest and C. Stein
Data Structures and Algorithms by A. Aho and J. Hopcroft and J. Ullman