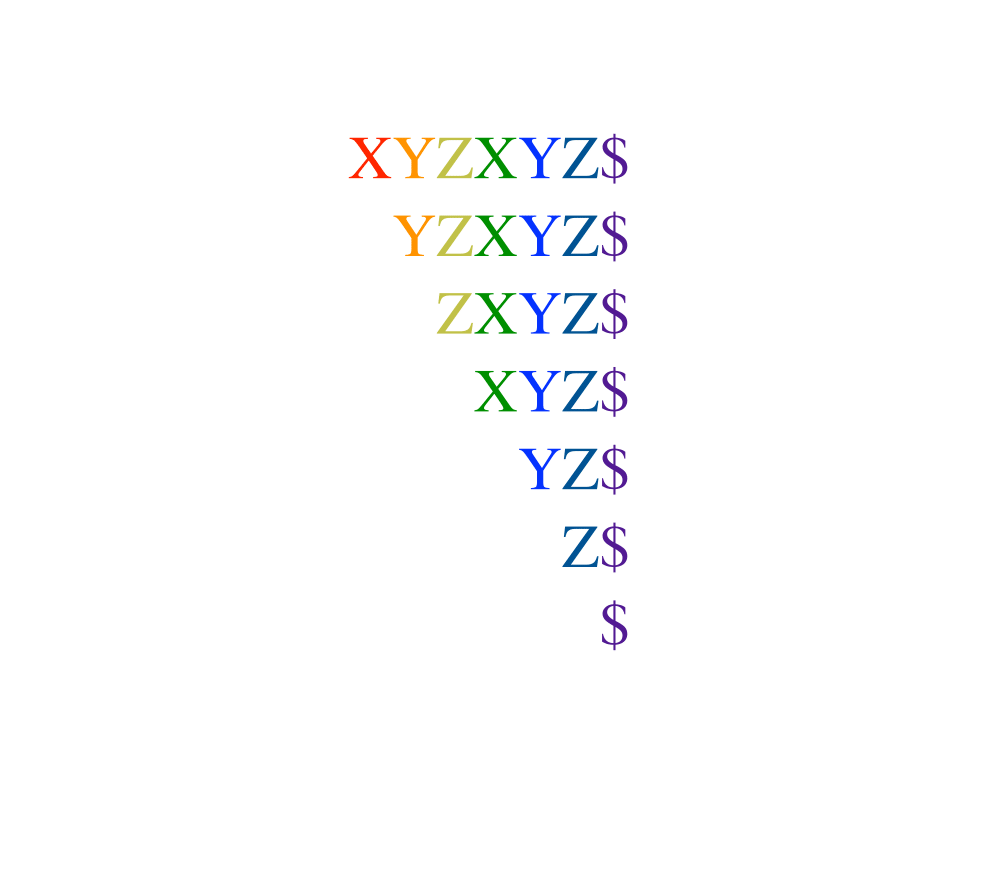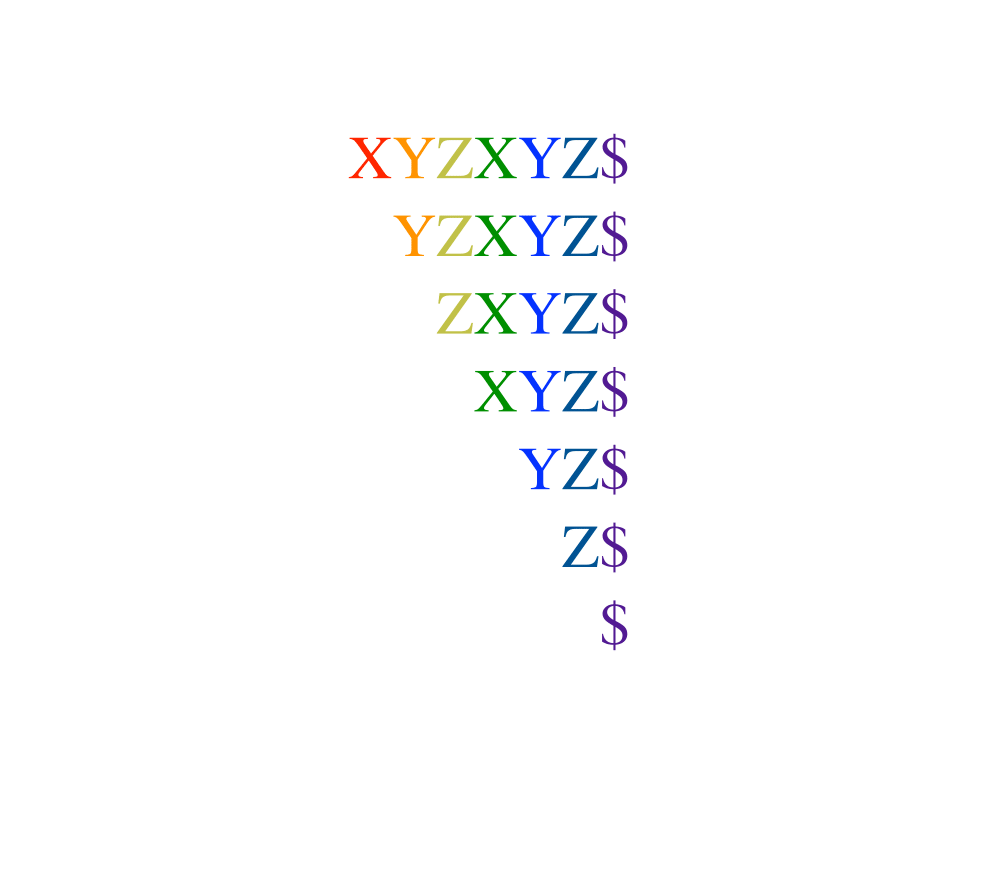 |
 |
|
|
Input Description: A reference string \(S\).
Problem: Build a data structure for quickly finding all places where an arbitrary query string \(q\) is a substring of \(S\).
Excerpt from The Algorithm Design Manual: Suffix trees and arrays are phenomenally useful data structures for solving string problems elegantly and efficiently. If you need to speed up a string processing algorithm from \(O(n^2)\) to linear time, proper use of suffix trees is quite likely the answer.
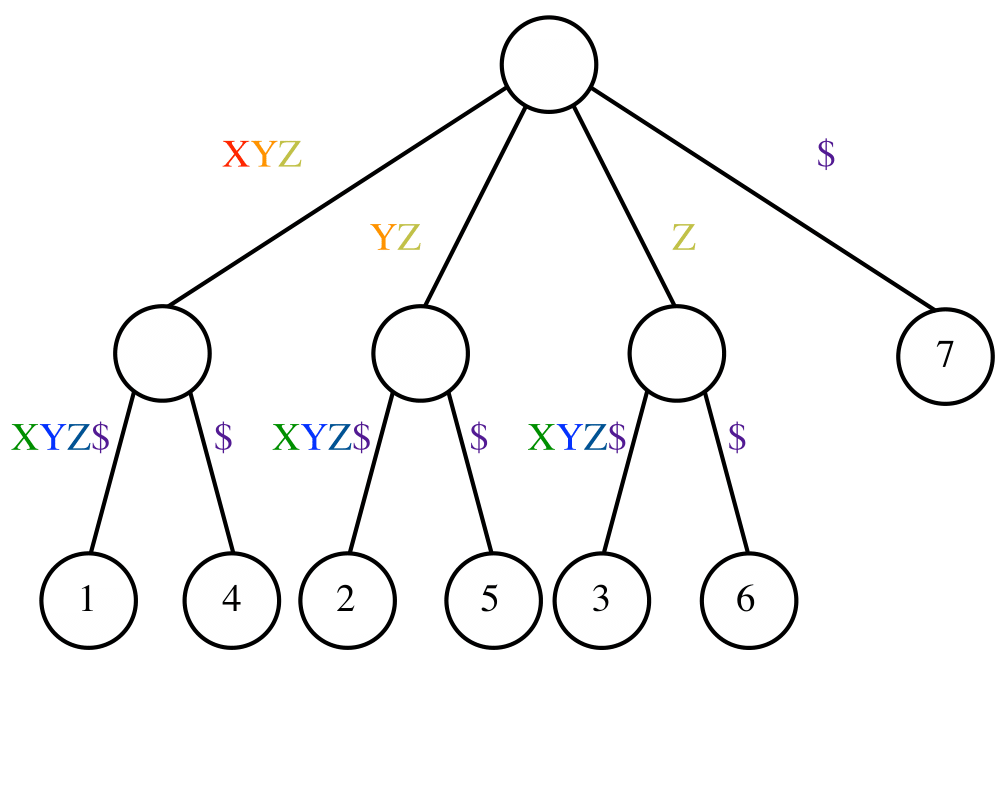
In its simplest instantiation, a suffix tree is simply a trie of the \(n\) strings that are suffixes of an \(n\)-character string \(S\).
A trie is a tree structure, where each node represents one character, and the root represents the null string. Thus each path from the root represents a string, described by the characters labeling the nodes traversed. Any finite set of words defines a trie, and two words with common prefixes will branch off from each other at the first distinguishing character. Each leaf represents the end of a string.
Tries are useful for testing whether a given query string \(q\) is in the set.
Starting with the first character of \(q\), we traverse the trie along the branch defined by the next character of \(q\). If this branch does not exist in the trie, then \(q\) cannot be one of the set of strings. Otherwise we find \(q\) in \(|q|\) character comparisons regardless of how many strings are in the trie. Tries are very simple to build (repeatedly insert new strings) and very fast to search, although they can be expensive in terms of memory.
A suffix tree is simply a trie of all the proper suffixes of \(S\). The suffix tree enables you to quickly test whether \(q\) is a substring of \(S\), because any substring of \(S\) is the prefix of some suffix (got it?). The search time is again linear in the length of \(q\).
 Data Structures and Algorithms by A. Aho and J. Hopcroft and J. Ullman |
  Longest Common Substring/Subsequence |
  Shortest Common Superstring |
  String Matching |
As an Amazon affiliate, I earn from qualifying purchases if you buy from links on this website.